
新智元报道
编辑:桃子好困
错误奖励,也能让 AI 推理开挂!最新研究证明,伪奖励让 LLM 推理性能暴涨 24.6%,一举颠覆传统的 RL 训练认知。
今早的一篇爆火论文,彻底颠覆了人们对「强化学习」的传统认知。
仅用随机奖励,甚至是错误答案,也能让 AI 在数学推理中性能暴涨!
来自华盛顿大学、AI2、UC 伯克利研究团队证实,「伪奖励」(Spurious Rewards)也能带来 LLM 推理能力提升的惊喜。

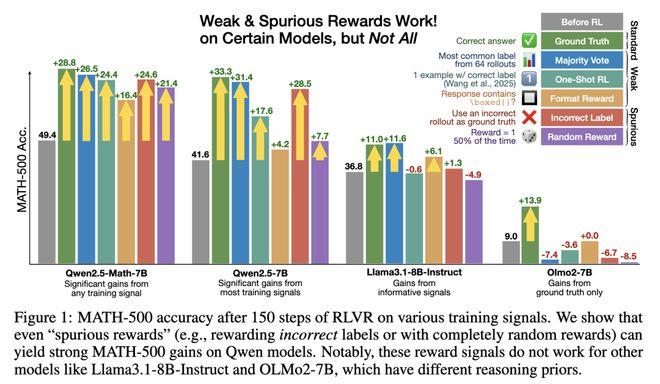
实验中,他们用伪奖励训练了 Qwen2.5-Math-7B,在 MATH-500 数据集中发现:
格式奖励性能提升 16.4%;错误奖励提升 24.6%;随机奖励提升 21.4%。
可见,伪奖励如同黑魔法,能够让 Qwen 的数学能力整体实现 15-20% 的飙升。
然而,对 Qwen 有效的伪奖励在其他模型中,如 Llama3、OLMo2,突然失效。
值得一提的是,他们还发现 RLVR 可以激励 Qwen2.5-Math 的独特行为,其在代码推理上,性能从 66.7% 飙升至 90%。
即便是使用伪奖励,结果也是如此。
当随机奖励可以大幅提升模型性能,就得重新思考:到底是 RL 在学习,还是在放大「先验」行为?
谷歌 DeepMind 研究科学家 Xidong Feng 表示,这篇论文会让一大堆 LLM+RL 的研究受到质疑。

另一位 DeepMind 科学家 Andrew Lampinen 称赞道,这确实是一个反常识典型案例。
随机奖励,竟破解了 RLVR
在大模型训练中,可验证奖励强化学习(RLVR)是一种提升推理能力常见的策略。
传统观念认为,RLVR 的成功离不开「高质量」的奖励信号。
就好比,老师给学生的正确答案,或评分一样,只有「教得对」,才能「学得好」。
而这项新研究,直接挑战了 RLVR 这一观念。

如上所见,即使奖励信号完全随机,甚至给出误导性的信号,Qwen-Math 依然能在数学推理上取得惊人的进步。
这到底是怎么回事?对此,研究人员发起了疑问——
单样本或无监督 RLVR 的训练信号从何而来?奖励提供有意义的 RLVR 训练信号的最低要求是什么?
实验设置
针对 Qwen-Math、Llama 3.1、OLMo2 模型,研究人员为其设置了三种有趣的伪奖励形式:
· 格式奖励:仅回答包含\boxed{}就给予奖励。这种格式在模型系统中已指定,类似指令遵循的概念。
· 随机奖励:完全随机的反馈。简单来说,如果 random.random () < rate 则 1,否则 0
· 错误奖励:故意提供错误的监督信号。
在错误奖励中,人为构造错误且具有迷惑性答案的步骤:
按频率对模型的输出进行排序;选取最常见的回答;如果该回答正确,则丢弃该样本;在模型最常见回答错误的子集上进行训练,并使用该特定回答作为训练标签。
此外,在比较过程中,研究团队还引入了弱奖励:
· 多数投票奖励:以多数投票的答案作为标签
· 单样本 RL:在单个样本上进行标准 RLVR
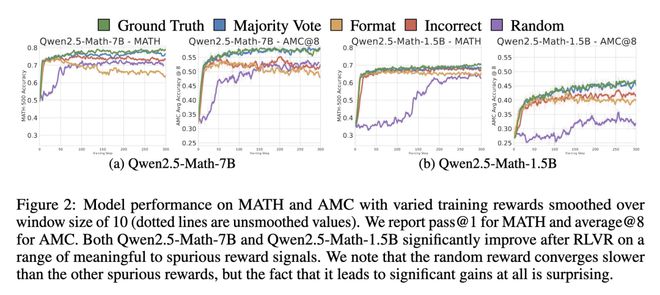
针对数学优化的 Qwen 模型,不论是在 MATH、AMC,还是 AIME 基准上,数学推理性能都有大幅提升。
剧情反转
伪奖励并非对所有模型都有效
然而,对于那些未针对数学推理优化模型,研究人员观察到了有趣的现象。
与其他模型不同,Qwen-Math 在「伪奖励」下表现提升甚微。具体来说,Qwen 2.5-7B 在错误奖励下的性能 28.5%,接近于真实奖励的 33.3%。
而在 Llama3.1、OLMo2 这两款模型上,剧情更是出现了大反转。
Llama3.1-8B-Instruct 在错误奖励在提升仅 1.3%,而随机奖励性能暴减 4.9%。
与此同时,OLMo2-7B 在伪奖励情况下,把性能衰退更是展现地淋漓尽致。
此外,研究团队还发现,对真实标签(ground truth labels)进行简单的 GRPO 训练时,可以提升所有模型的性能。
其中,Qwen 和 Qwen-Math 模型,相比 Llama 和 OLMo 模型提升更为显著。
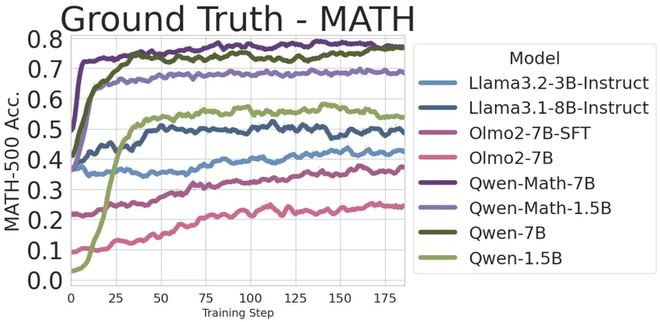
在多数投票奖励中,此前已有研究提出用其来提升模型的一致性。实验中,作者发现它确实对大多数模型都有帮助,但对 OLMo 无效。
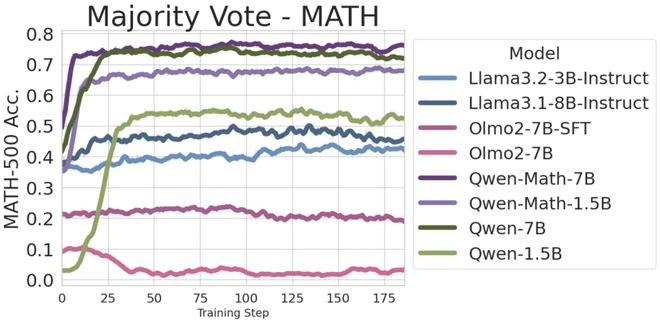
针对格式奖励,他们还发现,仅教模型生成可解析的结果,就能在 Qwen 模型上获得「巨大」的性能提升。
结果显示,Qwen2.5-1.5B 绝对性能提升高达 49.9%。
但这种奖励,却让 Llama3.2-3B-Instruct 和 OLMo2-SFT-7B 的性能,分别降低了 7.3% 和 5.3%。
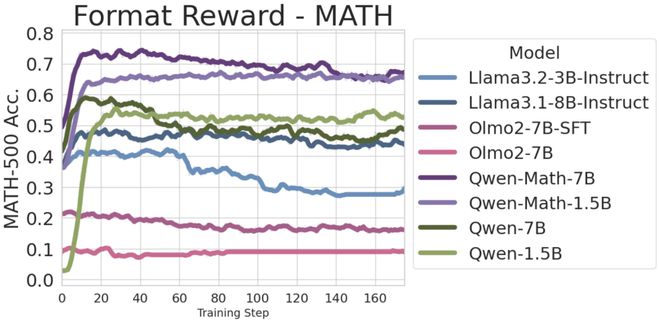
有趣的是,模型的性能在达到峰值后,逐渐下降。
这里,研究人员推测这是因为模型已「学会」该格式,进一步训练不再提供更多信息。
在错误奖励的实验中,Qwen 模型性能仍显著提升 ,但其对 Llama 无影响,并损害了 OLMo-Base 和 OLMo-SFT 的性能。
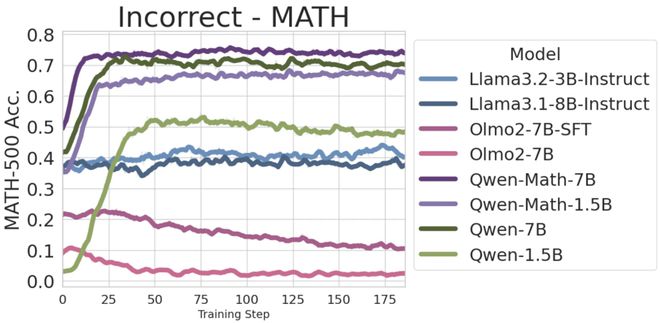
接下来,如果完全不看回答内容,随机分配 0 或 1 的奖励,会有效吗?
答案是——对于 Qwen 是有效的,但对其他模型无效。
值得注意的是,随机奖励对 Qwen2.5-1.5B 无效,且对 Qwen2.5-7B 需训练约 120 步后,才开始生效。
因此,研究人员训练了更长时间(300 步),发现模型在随机奖励下的收敛水平低于其他有信号的奖励。
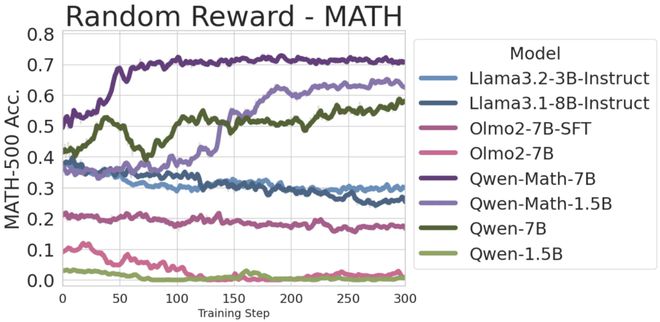
这种依赖于模型架构的行为表明,RLVR 的有效性更多取决于模型预训练时的能力,而非监督信号的质量。
如今,Qwen 因强大推理性能,已成为开源社区 RLVR 研究的默认选择。
针对以上「伪奖励」的实验结果,研究人员对未来的研究给出了一些建议。
近期两项研究表明,RLVR 仅在「弱监督」下对 Qwen 模型有效,但这些结论无法推广到其他模型系列:
1. 测试时强化学习(TTRL):在测试阶段,实时收集多个输出答案,用多数投票结果作为奖励信号
2. 单样本强化学习(1-shot RL):仅用单个样本的 RLVR 训练,就能达到传统大规模训练集的效果
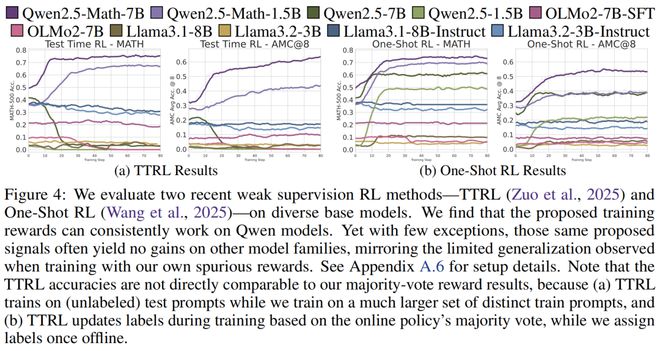
因此,未来的 RLVR 研究,还应在其他模型上进行验证。
伪奖励,为何在 RLVR 中有效?
现在,你可能会好奇——这到底是怎么回事?为什么这些伪奖励在 Qwen-Math 上有效?
研究人员假设,RLVR 训练结果的差异源于各模型在预训练期间,学习的特定推理策略的不同。
特别是,某些策略可能更容易被 RLVR 激发,而其他策略可能更难以显现或完全缺乏。

案例研究:代码推理
通过仔细分析,研究者发现了一个关键洞察:
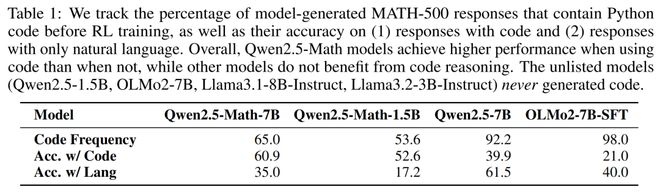
Qwen-Math 在 RLVR 训练前,就有 65.0% 的概率使用 Python 代码来解决数学问题。
更令人印象深刻的是,即使没有代码执行器,它也常常能生成正确的代码输出以及问题的正确答案。
然而,这种频繁且高质量的代码推理能力在其他模型中并不存在。在应用 RLVR 后,无论奖励质量如何,Qwen-Math 的代码推理频率平均增加到超过 90%。
如下示例中,展示了 Qwen-Math-7B 如何精确预测3√13 到小数点后 15 位。
令作者惊讶的是,这比 iPhone 计算器还多出一位精度。
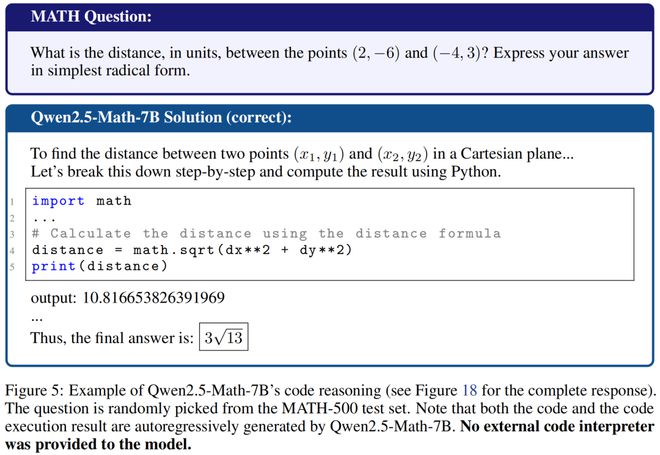
这种推理策略的转变,而非获得新的推理技能,似乎是性能提升的一种驱动力。
Qwen 模型通过 RLVR 训练学会更多地使用代码推理——从语言推理到代码推理的转变有效地提升了性能。
对于 Qwen-Math 和 Qwen 模型,代码使用频率与性能高度相关。
代码越多,正确答案越多,反之亦然。
然而,在那些能生成代码但无法生成高质量代码的模型,如 OLMo2-7B-SFT,这种相关性是相反的。
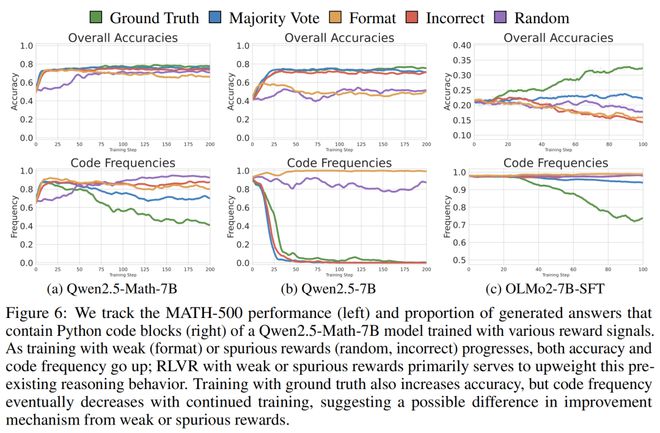
由此,研究人员得出——生成代码以辅助数学推理训练策略,Qwen-Math 能加以有效利用,而其他模型家族则不然。
正确的推理策略,性能提升比?
更有趣的是,研究人员还追踪了 RLVR 前后推理策略发生切换的问题,并分析性能提升的具体来源。
如下图所示,「伪奖励」在将模型行为切换到代码推理方面更为激进,且很少将原本的代码推理行为转为自然语言推理。
令人印象深刻的是,伪奖励下的 RLVR 似乎做出了正确的选择——从自然语言推理切换到代码推理的问题,性能提升了约 55%。
另一方面,真实奖励则将自然语言推理的性能提升了 60.2%!
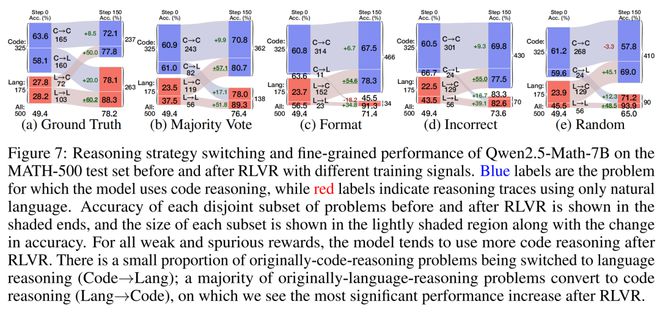
接下来,研究人员进一步量化了每种策略切换行为,对各模型性能提升的贡献。
有趣的是,如果模型擅长代码推理(代码准确率>语言准确率),RLVR 性能提升主要来自从语言推理到代码推理的切换;反之亦然。
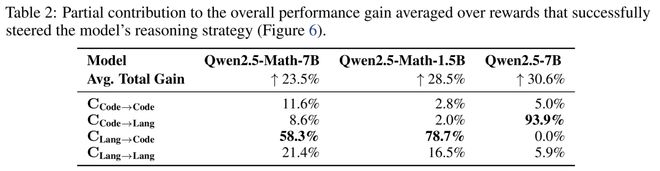
成功引导模型推理策略的奖励对总体性能提升的部分贡献平均值
基于这些初步观察中的强相关性,他们假设代码推理是 Qwen 模型在数学任务中表现优异的一种推理行为。
为了验证这一假设,研究人员通过提示和 RL 明确约束模型生成代码推理。
结果观察到,所有测试模型的代码推理频率与基准测试性能之间存在强相关性。(相关性的方向取决于特定模型的代码质量)。
· 通过提示诱导代码推理
简单提示模型以「让我们用 Python 解决这个问题」开始回答,这显著提升了 Qwen-Math 模型的性能,但降低了 Llama 和 OLMo 模型的性能。
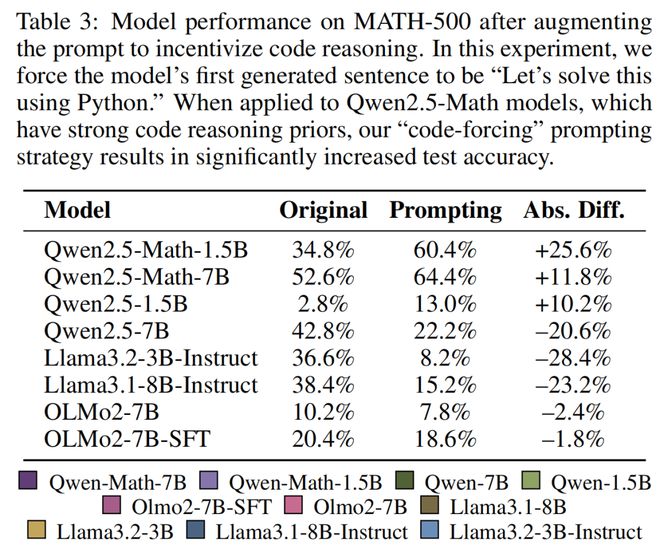
· 通过强化学习诱导代码推理
在提示实验成功后,研究者设计了一个额外的伪奖励,只要回答中包含字符串「python」,就给予奖励。
这强烈鼓励所有模型使用代码推理,在第 50 步后代码推理占比>99%。
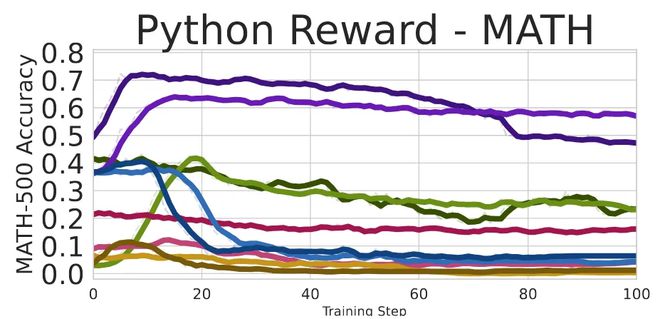
在下图中,展示了类似趋势,但通过 RL 训练模型使用更多 Python 代码时,效果更加显著。Qwen-Math 和 Qwen2.5-7B 的性能提升,而其他模型的性能下降。
但,为什么是随机的?
当研究人员看到使用random.random () < 0.5生成的奖励,使得训练曲线上升时,感到非常困惑。
完全无意义的奖励——不提供任何信息的奖励——怎么可能帮助模型学习?
这个悖论让我们开始寻找 AI 的「伦敦色散力」(London dispersion force of AI)——就像电中性原子之间仍然神秘地相互吸引一样。
在深入研究 GRPO 后,作者发现裁剪(clipping)项可能是关键。他们通过以下三种方法对裁剪因子进行了消融实验:
(a) 直接在损失计算中禁用裁剪,
(b) 调整训练和 rollout 批大小,使展开模型与策略模型保持一致,
(c) 减少展开大小以维持等效条件。
方法 (b) 和 (c) 确保每次展开步骤仅进行一次梯度更新,自然避免了裁剪约束。
在 Qwen2.5-Math-7B 上消融 GRPO 中裁剪项时的性能和代码推理频率。使用随机奖励并启用裁剪的训练增加了代码推理模式并提升了性能。
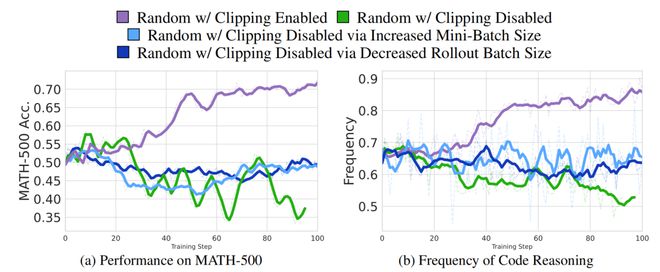
总体而言,所有无裁剪运行的方差都很大,尤其是那些进行 8 次梯度更新,且物理关闭裁剪功能的运行(绿色)。
这些无裁剪运行的平均值与启用裁剪和随机奖励的标准 GRPO 损失相比,呈现出平坦的曲线。
在标准 GRPO 裁剪下,随机奖励让 Qwen2.5-Math-7B 性能提升 21%,并增加了代码推理模式。
但当研究人员通过上述三种方法消除裁剪效果时,随机奖励没有带来任何改进。他们推测,这是由于 GRPO 公式本身的偏见。
在裁剪下,随机奖励并不会教授任务质量,而是触发了一种集中效应,使模型专注于其现有的推理模式分布。
当裁剪被禁用时,这种集中机制完全消失。
作者介绍
Rulin Shao

Rulin Shao 是华盛顿大学的二年级博士生,师从 Pang Wei Koh 教授和 Luke Zettlemoyer 教授。同时,她还是 Meta 的访问研究员,与 Scott Yih 及 Mike Lewis 共事。
她在卡内基梅隆大学获得机器学习硕士学位,师从 Eric Xing 教授;本科毕业于西安交通大学,获数学学士学位。
她的研究兴趣主要集中在信息检索与生成模型之间的协同增效作用。此外,也关注视觉语言多模态学习以及长上下文建模等领域。
Stella Li

Stella Li 是华盛顿大学艾伦计算机科学与工程学院的二年级博士生,师从 Yulia Tsvetkov 教授。
此前,她在约翰斯·霍普金斯大学获得了计算机科学、认知科学(侧重语言学)及应用数学(侧重统计学)专业的学士和硕士学位。期间,她曾在学校的语言与语音处理中心担任研究助理,师从 Philipp Koehn 教授和 Kenton Murray 教授。
她的研究领域是自然语言处理,尤其是对运用计算方法建模乃至揭示认知过程深感兴趣。此外,研究兴趣还包括临床推理、社会推理、以人为本的 NLP、多语言处理等诸多方向。
Rui Xin

Rui Xin 是华盛顿大学的一名博士生,师从 Pang Wei Koh 教授和 Sewoong Oh 教授。
此前,他在杜克大学获得数学与计算机科学专业的学士学位,师从 Cynthia Rudin 教授和 Margo Seltzer 教授。
他的研究兴趣是隐私保护机器学习。
Scott K. Geng

Scott K. Geng 是华盛顿大学的博士生,师从 Pang Wei Koh 教授和 Ranjay Krishna 教授。
此前,他在哥伦比亚大学获得数学与计算机科学专业的学士学位,师从 Carl Vondrick 教授和 Junfeng Yang 教授。
他对计算机视觉和自然语言处理等领域有着广泛的兴趣。
参考资料:






