鱼羊发自凹非寺
量子位公众号 QbitAI
数学“猜想界皇冠”黎曼猜想,刚刚取得全新突破!
成果来自 Larry Guth(拉里·古斯)和 James Maynard(詹姆斯·梅纳德)——
后者正是那位初出茅庐就让陶哲轩赞不绝口,因优化张益唐“孪生素数猜想”结果一战成名,并于 2022 年斩获菲尔兹奖的天才数学家。

陶哲轩第一时间在社交媒体上转发了他们的新论文:古斯和梅纳德在黎曼猜想方面取得了显著突破(尽管距离完全解决这个猜想还很远)。
他们对阿尔伯特·英厄姆在 1940 年给出的黎曼ζ函数零点的界进行了首次实质性改进(更广义地说,是控制各种狄利克雷级数的大值)。
实质性改进零点密度估计
论文标题是《New large value estimates for Dirichlet polynomials》(狄利克雷多项式的新大值估计)。
简单来说,古斯和梅纳德的新成果,就是证明了狄利克雷多项式取大值的频率的新界限。
狄利克雷级数的大值问题在解析数论中有广泛而重要的应用。比如,黎曼ζ函数就可以表示为一个狄利克雷级数,其非平凡零点的分布,与ζ(s)在临界线附近的大值密切相关。
根据陶哲轩的科普,令N(σ,T)表示实部至少为σ、虚部至多为T的黎曼ζ函数的零点数量。黎曼猜想告诉我们,对于任意σ>1/2,N(σ,T)都是0。
黎曼猜想目前还没办法无条件地证明,次优的选择是证明零点密度估计,也就是对N(σ,T)给出一个非平凡上界。这里σ=3/4 是一个关键值。
1940 年,英厄姆得到了一个界,即:
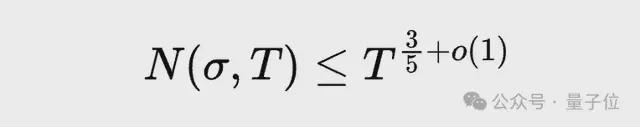
此后的八十年中,数学界一直未能对这个界限有实质性的改进,大部分工作只是对o(1) 误差动动脑筋。
这就限制住了数学家们对解析数论的探索,比如,受限于英厄姆界,为了在(x,x+x^θ)形式的几乎所有短区间内得到一个好的素数定理,长期以来数学家们只能处理θ>1/6 的情况。
现在,古斯和梅纳德成功将3/5=0.6 提高到了 13/25=0.52。还是拿上面这个例子来说,θ的范围就可以从θ>1/6=0.166…提高到θ>2/15=0.133…(黎曼猜想下θ>0)。

论文的论证主要基于傅里叶分析。陶哲轩指出,前几个步骤属于标准步骤,许多数学家包括陶哲轩自己都能想到。
但这一次古斯和梅纳德做了一些“巧妙且意想不到”的选择,包括:
- 将一个关键的相位矩阵 n^(it)=e^(itlogn) 提高到了 6 次方。
- 没有使用平稳相位方法来简化傅里叶积分。
他们根据狄利克雷级数的大值点位置,将问题分为加性能量E(W)小、中、大三种情况,并通过参数的变化来处理每种不同情况。
其中,狄利克雷级数中隐含的相位函数 tlogn 的精确形式变得非常重要。
这是一种出人意料的方式,利用了解析数论中出现的指数和的特殊性质,而不同于人们在调和分析中可能遇到的更一般的指数和。
菲尔兹奖和数学新视野奖得主们
詹姆斯·梅纳德的名字,关心数论的朋友们想来都不陌生。
作为当今数学界最闪耀的明星之一,他一路斩获拉马努金奖、柯尔奖,并在 2022 年获得数学界最高奖菲尔兹奖,和 2023 科学突破奖下的数学新视野奖。

有意思的是,梅纳德的成名之路与华裔数学家们的名字紧密关联在一起。
26 岁时,他提出了一个完全独立的、比张益唐更强大的“孪生素数猜想”结果,因此声名鹊起。
而在此过程中,他又与陶哲轩发生了一段“惜才”美谈:梅纳德发表成果之前,得知大牛陶哲轩也在同一问题上,得出了基本相同的结果。但陶哲轩在看过他的证明方法之后,认为其方法比自己的更简洁。
出于惜才之心,陶哲轩主动放弃了和梅纳德联名发表这项研究的机会,以免自己的名气掩盖年轻数学家的成就。
梅纳德的战绩还包括,和 Dimitris Koukoulopoulos 合作攻克 80 年数学难题 Duffin-Schaeffer 猜想,和 Thomas Bloom 合作改进最著名的无平方差集界限等等。
目前,梅纳德在牛津大学任教授。
拉里·古斯是 MIT 的克劳德·香农数学教授,同样是一位数学新视野奖得主,他还获得过塞勒姆奖、克莱研究奖等奖项。
他在几何学、调和分析、拓扑学和组合学领域造诣颇深。2021 年当选为美国国家科学院院士。

有点遗憾的是,拉里·古斯已经 47 岁,对于菲尔兹奖而言已经“超龄”(菲尔兹奖只颁发给 40 岁以下数学家)。
One More Thing
古斯和梅纳德的新论文一经发表,已经引发了不少关注。
网友们的热烈讨论中,同样有不少信息值得参考。
有网友 po 出了ζ函数的可视化网页,可以帮助理解新论文的内容。

而如果你对梅纳德其人其研究感兴趣,参考链接网友们也已总结到位了:
https://news.ycombinator.com/item?id=40571995
论文地址:
https://arxiv.org/abs/2405.20552
参考链接:
[1]https://mathstodon.xyz/@tao/112557249982780815
[2]https://news.ycombinator.com/item?id=40571995
— 完 —






