
人们一直以为,大模型的隐藏状态是抽象的“语义压缩”。但这篇论文发现,Transformer 并没有丢掉任何输入信息——它能凭隐藏状态精确反演出你说的每一个字。
来源:PaperWeekly
我们一直以为,语言模型的隐藏状态是对输入的一种“压缩”或“抽象”。在这层抽象里,模型似乎丢掉了表面信息,只保留“语义精华”——这就是我们所说的“理解”。
但这篇论文颠覆了这个想法。作者发现,在标准的 Transformer 结构下,模型的最后一 token 隐状态几乎必然能唯一确定输入序列。
换句话说,只要你知道这个隐藏状态,就能反推出原文。而且,这个性质不仅在随机初始化时成立,在整个训练过程中也不会被破坏。
更令人震撼的是,他们没有停留在数学证明,而是进一步提出了一个实际算法——SipIt(Sequential Inverse Prompt via Iterative Updates)。它不需要任何外部模型训练,仅凭 Transformer 的隐藏状态,就能把输入一个 token 一个 token 地完整还原。
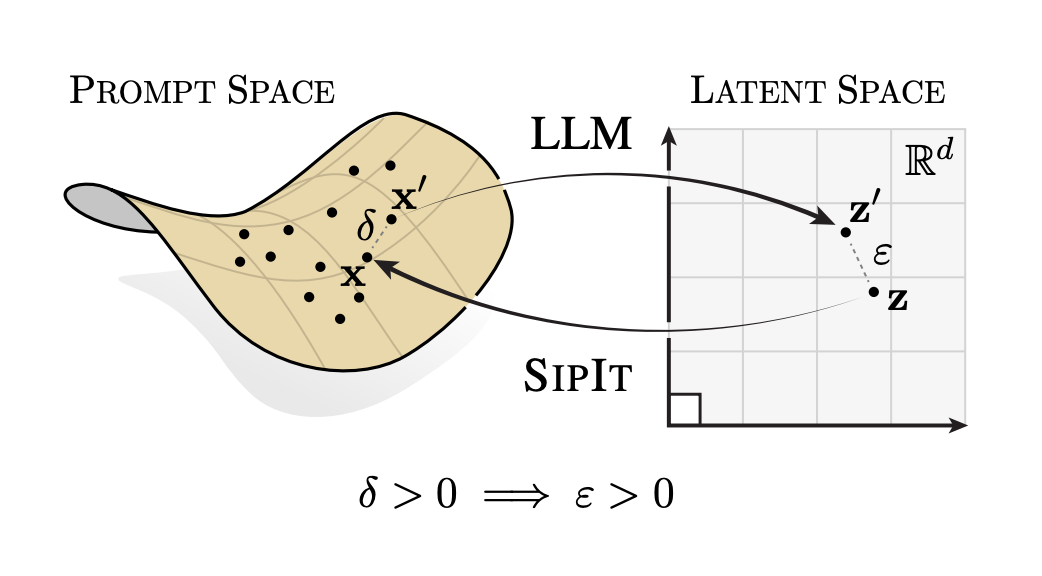
▲ 图 1. Prompt 到 Latent Space 的单射映射:可视化 Transformer 将输入映射到隐空间,并通过 SIPIT 完整反演。

论文链接:Language Models are Injective and Hence Invertible

研究背景:为什么单射性如此重要?
在 Transformer 的每一层里,我们都能看到“似乎会丢信息”的环节:LayerNorm 会重标尺度,残差连接可能抵消特征,注意力层还会把多个 token 混合成一个上下文表示。这些操作看起来都不利于可逆性。
然而作者从另一个角度切入——解析性(real-analyticity)。他们将 Transformer 视为从离散序列到连续表示的解析映射:
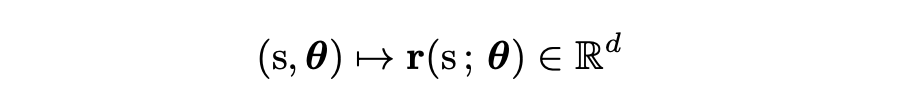
这里是输入 token 序列, 是模型参数, 是最后一 token 的隐藏状态。
作者进一步形式化地指出,这个映射几乎处处是单射的:
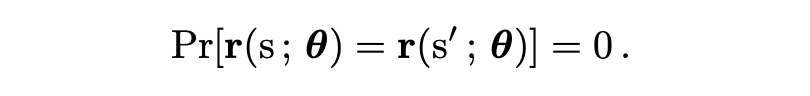
也就是说,不同输入序列映射到相同隐藏状态的概率为零。解析函数的零点集要么处处为零,要么测度为零。这意味着,只要存在一个参数配置让两个不同输入产生不同输出,几乎所有参数下都不会“撞车”。
于是作者定义了一个碰撞检测函数:
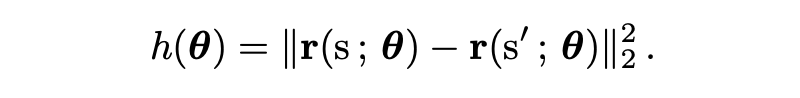
只要存在某个 让 ,那就意味着“不同输入映射成相同隐藏态”的概率为零。
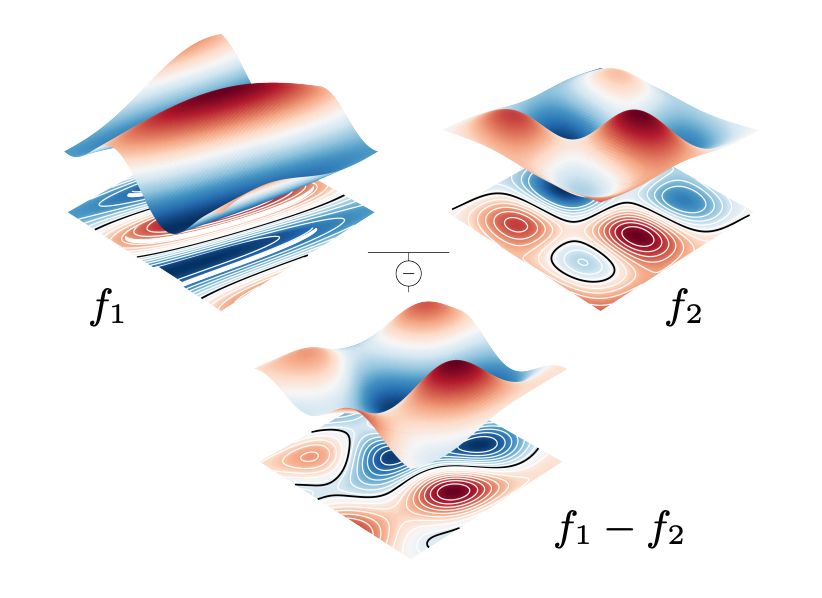
▲ 图 2. 零测集的可视化直觉:零点集合只形成细线(meaure zero),说明碰撞几乎不可能发生。
他们进一步证明:即使经过有限步梯度下降,这种性质仍然保持。因为参数更新:
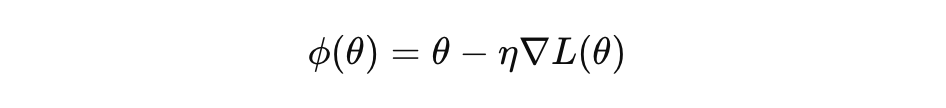
本身也是解析函数,其雅可比行列式非零,不会把空间“压塌”。更严格地,他们给出了如下结论:
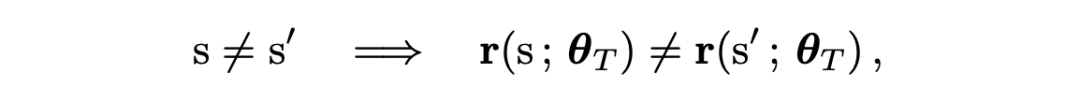
也就是说,在有限步梯度下降(步长 )后,模型依然保持输入到隐藏空间映射的单射性。
这表明,Transformer 的可逆性是整个训练过程的结构性特征,而非偶然现象。

方法:SipIt 如何“倒放”Transformer?
有了理论基础,作者提出了一个问题:
如果隐藏状态真的能唯一对应输入,我们能否直接把原文还原回来?
他们的答案是——可以。
核心思路
作者定义了函数 ,其中 表示前缀序列。也就是说,每个位置的隐藏状态由前缀和当前 token 唯一决定。
因此,已知隐藏状态 ,我们可以遍历词表 ,寻找唯一满足 的 token。只要找到这个 token,就能确定当前位置的输入。

▲ 图 3. SIPIT 反演伪代码:逐位反演输入的迭代流程,仅依赖隐藏状态即可完成重建
SipIt 基于这个原则逐位反演输入:从第一个 token 开始,对候选词按策略遍历,当匹配的隐藏状态落入允许的 ε 邻域(ε-ball)时即接受,并进入下一位。
作者在文中指出:“在实践中,我们接受那些观测隐藏状态位于预测值 ε 球邻域内的匹配结果。” 这种基于容差的检查方式保证了算法在有限步内收敛并找到唯一匹配。
当所有位置都验证完毕,SipIt 即可还原出完整输入 。理论上时间复杂度为线性,最坏情况下也不超过 步,即保持线性时间复杂度(linear-time bound)。
SipIt 把“单射性”从一个理论命题变成可操作事实——能否被 SipIt 完整反演,就是模型是否真正保留信息的实证检测。

实验结果:模型真的没丢信息吗?
作者在 GPT-2 Small、Gemma-3、Llama-3.1、Mistral-7B、Phi-4-mini 等多种架构上做了验证。他们为每个模型计算不同输入的最后一 token 表示之间的最小距离。
结果显示,所有最小距离都远高于 ,说明几乎不存在碰撞。
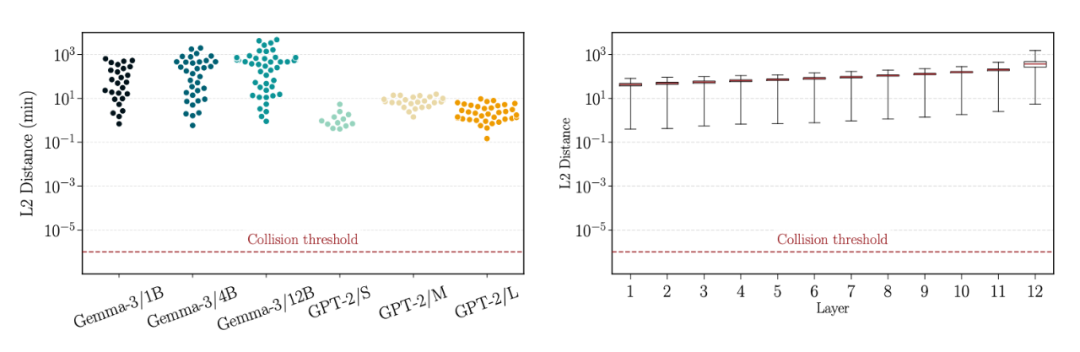
▲ 图 4. 不同层间的最小距离始终高于阈值,未出现重叠
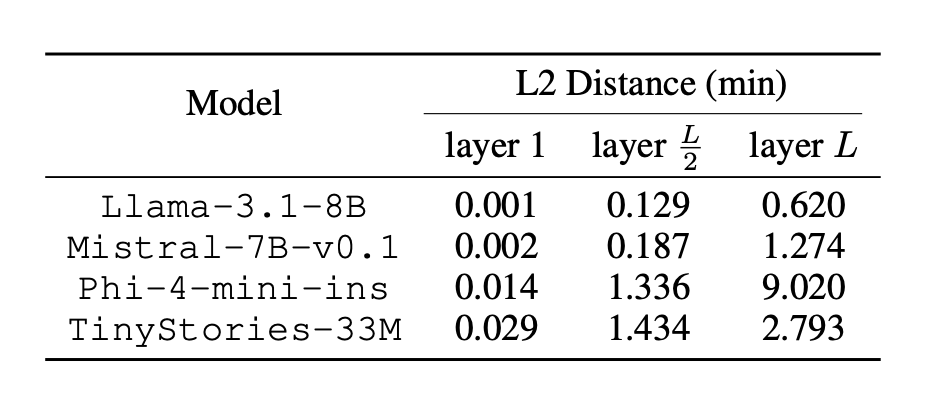
▲ 表 1. 不同模型的距离分布均明显高于碰撞阈值
极限穷举测试:仍未出现碰撞
为避免采样偏差,作者挑出最相似的 10 对前缀,并穷举词表的所有接续组合——相当于检索上千亿条输入。即便在这个极端测试下,隐藏状态的最小距离依然大于 0。
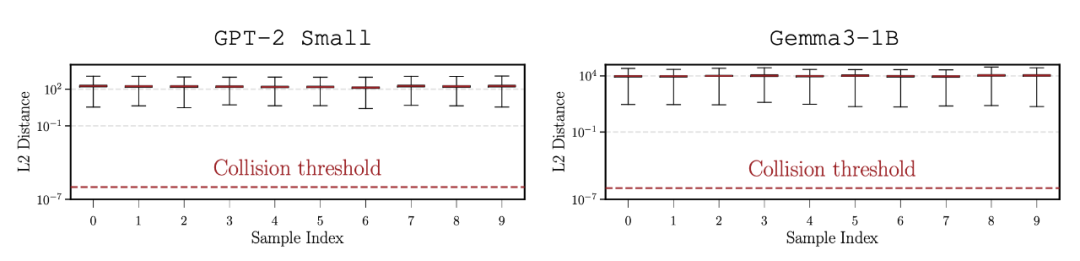
▲ 图 5. 在极限应激测试下,所有最小距离仍远高于零
他们还观察了距离随序列长度变化的趋势:短句在前几层迅速拉开间距,长句则趋于稳定。
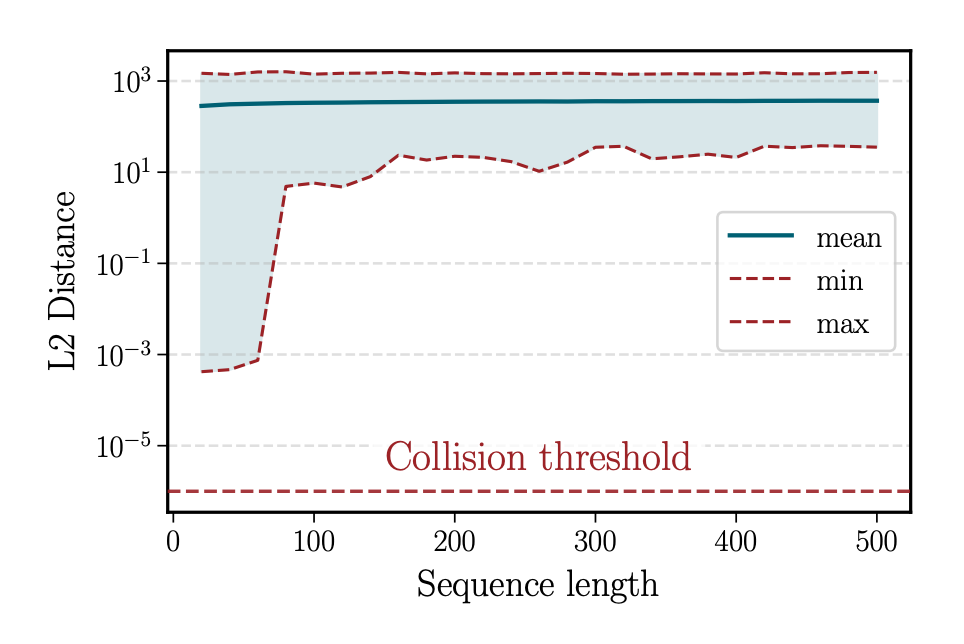
▲ 图 6. 短序列距离上升更快,长序列趋于稳定
反演实验:SipIt 的可行性验证
在 GPT-2 Small 上,作者选取 100 条提示序列,仅使用隐藏状态进行反演。SipIt 实现了 100 % token-level 精确恢复,反演耗时与序列长度线性增长。
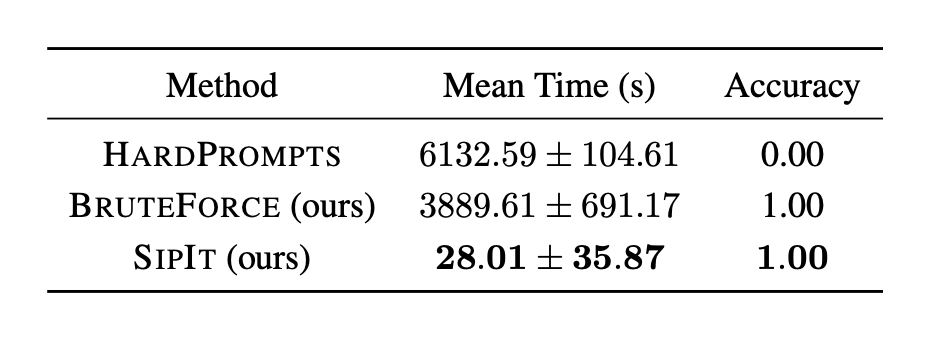
▲ 表 2. SipIt 在保持 100% 精度的同时速度领先百倍
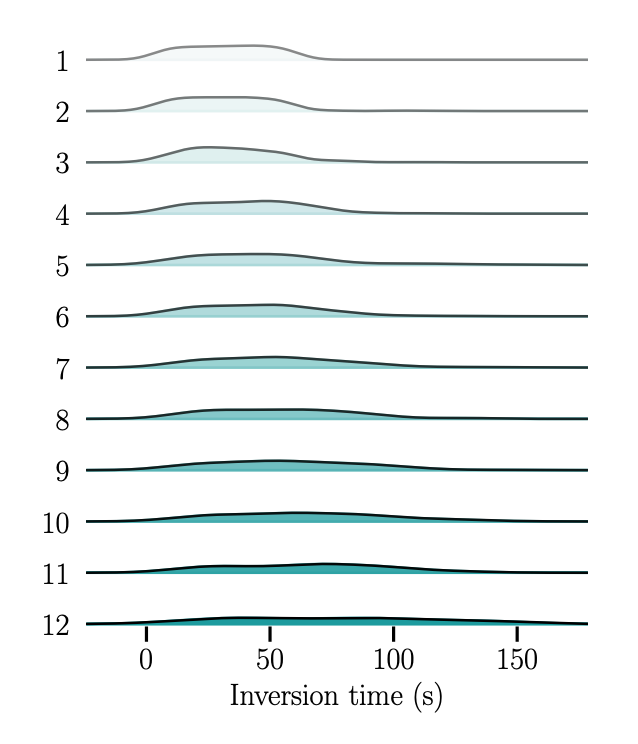
▲ 图 7. 反演耗时随层深度缓慢上升,整体呈线性增长

总结
这项研究并未改动模型结构,却动摇了我们对“隐藏表示”的长期假设。Transformer 的最后一 token 隐藏状态在解析意义上几乎处处可逆:不同输入有不同表示,训练过程不会破坏这种区分性。
SipIt 把理论转化为工具——在不训练任何外部网络的前提下,仅凭隐藏状态就能线性时间重建原文。
从科研角度,这为解释 LLM 内部表征提供了坚实起点;从工程角度,这提醒我们:缓存隐藏状态等价于缓存用户输入,隐私治理必须覆盖这一层;从方法论角度,它展示了一种范式——先证明结构,再把结构做成算法。
也许我们需要重新定义“理解”与“记忆”的界限。 至少从这篇论文的结果看——LLM 没有忘记你说过的每一个字。






