新智元报道
编辑:犀牛
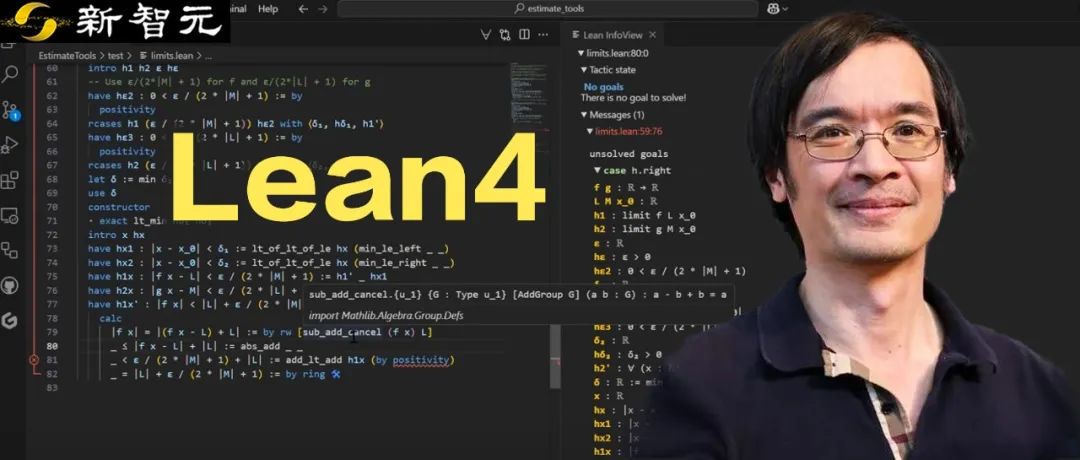
数学大师陶哲轩的第三支 Lean 4 自动化数学证明视频来了!他携手 GitHub Copilot 挑战分析学经典的「ε-δ」极限问题:加法定理 Copilot 挥洒自如,减法开始卡壳,乘法更是全面失控。Copilot 究竟是神助攻还是添乱?
数学大师陶哲轩的 AI 新实验来了!
这次是 Lean 4 自动化数学证明的第三支视频。
主要看看 GitHub Copilot 在处理分析学经典的「ε-δ」问题(描述函数极限的经典方法)时,效果究竟如何。
之前,陶哲轩上传了两支这个系列的视频。
加上此次的一共 3 支视频,陶哲轩的油管频道已经有 1.7 万位订阅者了。
看来,他作为菲尔兹奖得主、当代最杰出数学家之一的影响力的确毋庸置疑。
陶哲轩在此次定理形式化演示中发现,GitHub Copilot 在帮助新手入门和处理基础任务时表现得相当不错。
它能帮助用户快速上手 Lean 语言(一种交互式定理证明工具),提供语法提示,并智能补全基本定义和声明。
在比较简单的证明,比如函数极限的和定理中,Copilot 还能准确预测证明结构和关键步骤,表现得就像个得力助手一样。
但当证明变得复杂时,Copilot 的短板就暴露出来了。
比如在处理函数极限的差和积定理时,它在复杂的代数推导、寻找合适的数学引理(比如与绝对值相关的引理)等方面显得力不从心。
Copilot 有时还会出现「幻觉」,生成压根不存在的策略,或者犯一些低级错误,导致证明过程乱成一团。
这时,陶哲轩不得不亲自出马,修正错误,甚至完全接管证明。
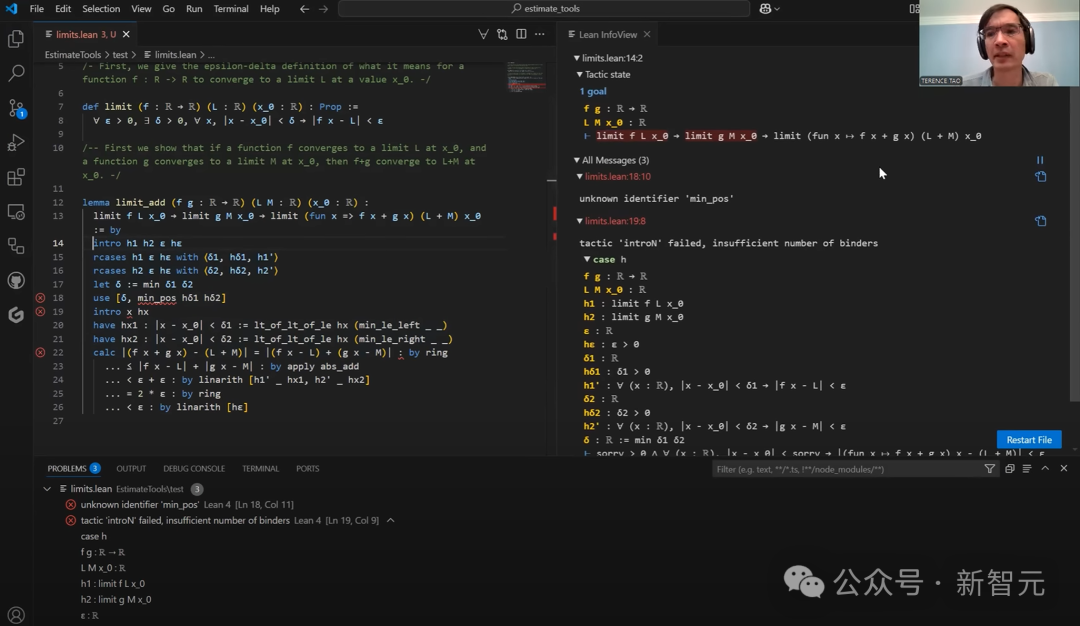
「人机协作」的证明过程
形式化数学的目标是用计算机能完全看懂的精确语言,把数学概念和证明写出来,再用定理证明工具(比如视频里提到的 Lean)来一步步检查推理是否靠谱。
这就像把数学证明翻译成一种特别严谨的编程语言。
第三弹的视频里,陶哲轩从一个经典的分析学概念入手:函数的极限。
用 Lean 把这个定义写出来,对新手来说真不是件容易事儿。不过,GitHub Copilot 就像个贴心助手,派上了大用场。
陶哲轩刚敲下「定义一个谓词 limit f x₀ l」,Copilot 就立刻 get 到他想表达的是「ε-δ」极限定义,秒秒钟生成了对应的 Lean 代码。

虽然陶哲轩根据自己的习惯稍作调整,但 Copilot 的智能补全明显让整个过程快了不少。
「和的极限」——小试牛刀
接下来,陶哲轩挑战了一个更复杂的定理:如果函数f(x)的极限是L,g(x)的极限是M,那么f(x) +g(x)的极限就是L+M。
Copilot 又秀了一把操作。它不仅帮陶哲轩写出了定理的 Lean 声明,还开始「猜」证明的步骤,建议引入假设,提取出ε和δ这些关键变量。
Copilot 尝试用 Lean 的 calc 块整理不等式链,还试着用 simp 简化表达式。
但这里它开始出小差错,比如搞乱了绝对值的位置,或者在代数推导时显得不够「机智」。
陶哲轩不得不出手,比如他提醒 Copilot 用「ε/2」技巧。Copilot 虽然一开始没完全跟上,但调整后成功融入了这个思路。
最终,经过一番人机配合,这个「和的极限」定理在 Lean 里被顺利证明通过。
陶哲轩觉得,Copilot 干了大部分活,互动体验也很不错。
「差的极限」——AI 有点懵
有了「和的极限」的经验,陶哲轩以为「差的极限」会同样顺利。这个定理是说,如果f(x)的极限是L,g(x)的极限是M,那么f(x)-g (x)的极限是L-M。
Copilot 似乎也信心满满,直接套用了「和的极限」的证明套路,甚至用上了上述的「ε/2」的技巧。
但过程中,Copilot 还是卡壳了,甚至还「脑补」了一个 Lean 里根本不存在的策略(叫什么 sub subanc)。
面对 Copilot 的「胡思乱想」,陶哲轩试图给予提示,但 Copilot 还是搞不懂。
陶哲轩意识到,这些代数变换对人类来说简单,但在 Lean 里需要调用特定的数学引理来支撑每一步。最终,陶哲轩只能亲自动手完成这些代数推导。
这一关让陶哲轩看到,Copilot 虽然能模仿证明的大框架,但在需要特定引理或复杂代数操作时,容易掉链子。
他给 Copilot 这一关的表现打了个B+:帮了不少忙,但关键时刻还是得靠人类引导甚至接管。
「积的极限」——彻底乱套
最难的来了:如果f(x)的极限是L,g(x)的极限是M,那么f(x)·g(x)的极限是L·M。
这个证明比加减法复杂多了,尤其在控制误差(ε)时,堪称噩梦。
Copilot 尝试沿用标准套路,加中间项、三角不等式。
但问题来了,Lean 里处理绝对值乘积或求和,需要非常具体的引理,比如把|ab|变成|a||b|得用 abs_mul,|a+b|≤|a|+|b|得用 abs_add。
Copilot 在找这些引理时频频出错,甚至想用一些通用的策略(比如线性算术),却因为有乘法和绝对值而行不通。
更麻烦的是,为了让误差控制在ε内,一开始得精心设计f(x)和g(x)的误差参数。这些参数选择和边界估计对 Copilot 来说有点太难了,它试了些参数,但证明中发现行不通,甚至还差点弄出除以零的错误。
陶哲轩在这阶段花了大量时间「救火」,不断调整 Copilot 的尝试,寻找正确的引理,甚至回去改最初的误差参数。
整个过程乱成一团,尽管 Lean 系统改参数相对方便(改了让系统重查就行),但得对证明结构有清晰理解才知道怎么改。
最终,经过艰苦努力和大量人工干预,陶哲轩完成了「积的极限」证明。
他总结说,一旦证明复杂到一定程度,Copilot 就变得「不怎么靠谱」了。
证明的完整代码在 GitHub 中:
import Mathlib /- In this file we are going to give some "epsilon-delta" proofs of facts about limits of functions on the real line. -/ /- First, we give the epsilon-delta definition of what it means for a function f : R -> R to converge to a limit L at a value x_0. -/ def limit (f : ℝ → ℝ) (L : ℝ) (x_0 : ℝ) : Prop := ∀ ε > 0, ∃ δ > 0, ∀ x, |x - x_0| < δ → |f x - L| < ε /-- First we show that if a function f converges to a limit L at x_0, and a function g converges to a limit M at x_0, then f+g converge to L+M at x_0. -/ lemma limit_add (f g : ℝ → ℝ) (L M : ℝ) (x_0 : ℝ) : limit f L x_0 → limit g M x_0 → limit (fun x => f x + g x) (L + M) x_0 := by intro h1 h2 ε hε -- Use ε/2 for each function have hε2 : 0 < ε / 2 := half_pos hε rcases h1 (ε / 2) hε2 with ⟨δ₁, hδ₁, h1'⟩ rcases h2 (ε / 2) hε2 with ⟨δ₂, hδ₂, h2'⟩ let δ := min δ₁ δ₂ use δ constructor · exact lt_min hδ₁ hδ₂ intro x hx ...
代码地址:
https://github.com/teorth/estimate_tools/blob/master/EstimateTools/test/limits.lean
有意思的是,大部分观众都觉得视频做得很棒,不过不少网友都建议陶哲轩换个新麦克风,以消除回音。
AI 只是副驾驶
在视频的最后,陶哲轩总结道:当证明过程变得复杂时,不如回到最传统的「人脑」方式——拿支笔在纸上把证明的思路和关键步骤理得清清楚楚,再去证明器里一步步形式化。
Copilot 更像是你的「得力助手」,适合在你已经大致知道证明方向时,帮你快速搞定那些重复的、格式化的工作。
它是个超强的辅助工具,但证明的策略、方向和最终验证,还是得靠人类自己来把控。
参考资料:






