
新智元报道
编辑:Aeneas 定慧
太震撼了,有开发者代码实证后发现,谷歌 AlphaEvolve 的矩阵乘法突破,被证明为真!Claude 辅助下,他成功证明,它果然仅用了 48 次乘法,就正确完成了4×4 矩阵的乘法运算。接下来,可以坐等 AlphaEvolve 更「奇点」的发现了。
就在刚刚,有人用 Claude 写代码证实——
谷歌 DeepMind 的 AlphaEvolve 求解矩阵乘法的突破,100% 正确!
即使已经过去好几天,AI 圈依然有许多人沉浸在这个 AI 的余震中。
在时隔半个世纪(56 年)后,AlphaEvolve 将4×4 的复数矩阵计算次数,从 1969 年 Strassen 的 49 次减少到了 48 次。

这相当于百米世界纪录从 9.58 秒挤进 9.57 秒——虽然只有百分之一秒,却再一次刷新人类极限的认知。
不过也有较真的人发出疑问了:AlphaEvolve 这个发现保真吗?
一位不信邪的开发者小哥,花了一整天时间,用代码来验证了一番。
结果,他真的眼看着这个矩阵乘法突破的算法,在自己眼前运行了起来。那一刻,简直太震撼了!
AlphaEvolve 的巨大威力,果然诚不我欺。如今,就差一个值得 AI 发现的想法,然后输入进去等着它去验证了。
现在,小哥已经发帖讲述了自己实证的具体过程,并在 GitHub 上上传了代码。
开源 Github 证明
谷歌 DeepMind 说的没错
具体来说,怎么验证这个算法真的有效呢?
小哥使用了 Claude 来帮忙。
首先,他实现了标准矩阵乘法(64 次乘法)和 Strassen 算法(49 次乘法)。
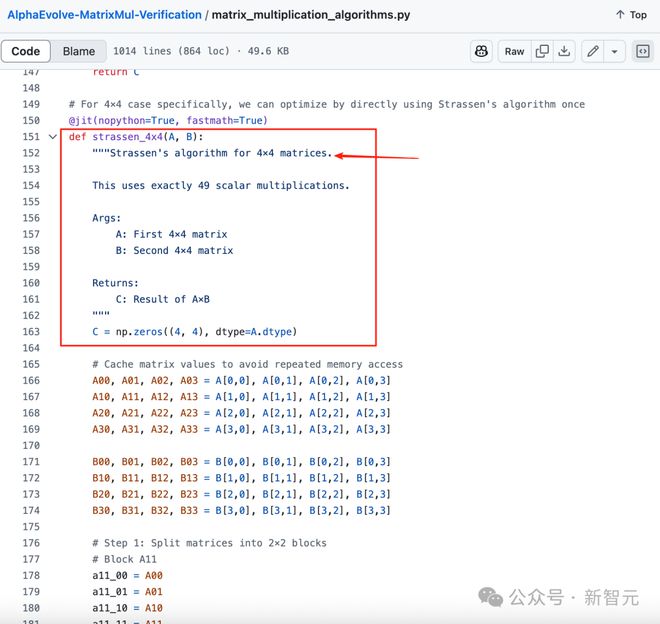
然后,他开始尝试用 DeepMind 论文中的张量分解,来实现 AlphaEvolve 算法。
但第一次,他碰壁了。一开始测试时,结果完全不对,数值误差非常大。
怎么办?小哥求助 Claude 后,它帮他理解了分解中使用的张量索引,并修复了实现中的问题。
然后,他用 Claude,自动将张量分解逆向工程,得出了直接的代码实现!

而代码的各项指标,都令人喜出望外。
无论是正确性、数值稳定性还是性能,各项指标都与 Google 论文中的官方报告保持一致!
-
正确性(对实值与复值 4 × 4 矩阵均能给出完全一致的结果)
-
数值稳定性(经优化后误差控制在机器精度,约 10⁻¹⁶)
-
性能(展平的直接实现速度领先原始张量式实现)
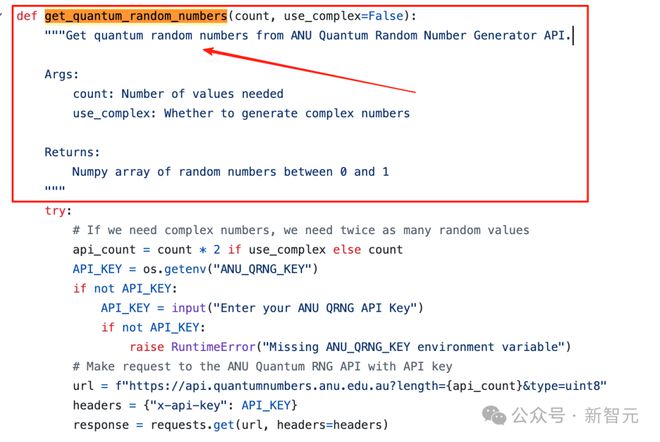
甚至,为了得到更有说明意义的结果,小哥使用了澳大利亚国立大学的量子随机数生成器提供的量子随机矩阵,来测试所有算法!
小哥上传 GitHub 的代码中,包括——
-
各种矩阵乘法实现(标准版、Strassen、AlphaEvolve)
-
一个张量分解分析器,用于反向解析算法
-
使用量子随机数进行验证和基准测试的代码
Github 地址:
https://github.com/PhialsBasement/AlphaEvolve-MatrixMul-Verification
目睹这个过程的网友们,也赞叹道,谷歌 AlphaEvolve 实在是太划时代了。
只是目前很多人还意识到,它的意义究竟有多重大,有多疯狂。
所以,AlphaEvolve 是怎样突破矩阵乘法难题的?
硬的来了
矩阵乘法难题是怎么解决的
如果想了解这个过程,就需要首先理解 AlphaEvolve 解决的这个问题——4 × 4 矩阵乘法的最小乘法次数。

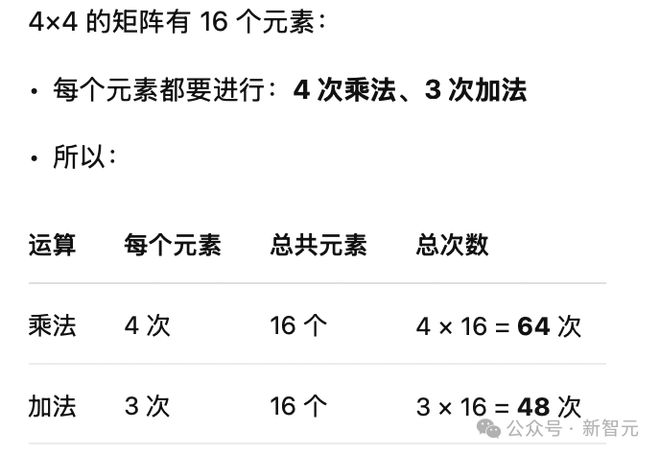
按照大一的「线性代数」,4 × 4 矩阵乘法按照传统的方法,需要64 次乘法计算 +48 次加法运算。
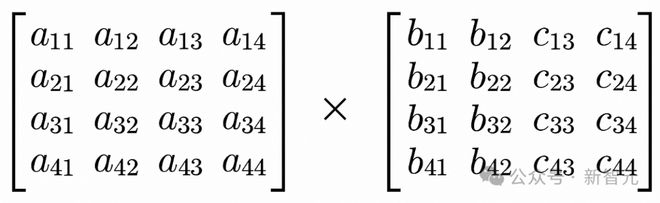
其实很好理解,以矩阵a第一行和矩阵b第一列的计算生成结果矩阵c的第一个结果为例,需要 4 次乘法运算和 3 次加法:

而结果矩阵依然是4×4,也就是 16 个元素,所以总得计算次数就是,64 次乘法和 48 次加法。
这种传统的办法被称为「标量乘法」,在硬件和能耗上远贵于加法,算法界把「减少乘法」当作衡量算法能力的第一指标。
我们都知道,现代计算机计算,都是把所有运算最终转化为了二进制的加减法。
如果能减少乘法运算次数,就能大大减少芯片最底层的开销。

这是最基础的、最底层的数学科学研究,如果能取得突破,将极大的影响芯片运算,进而影响整个计算机生态。
1969 年,Strassen 用两级递归将 4 × 4 矩阵乘法的计算从 64 减少到了 49 了,他是如何做到的?
Strassen 最早处理的是两个2×2 矩阵相乘,传统方法2×2 矩阵乘法要 8 次乘法。

Strassen 就想,既然结果C矩阵中每个数值都是类似「a*e+b*g」这样的排列组合,有没有能够减少乘法次数的办法?
结果,还真的让他给想出来了!
那就是「自定义」计算元素和序列,来组合出最终结果,如下图所示,比如设置 M3=a*(f-h),M5=(a+b)*h。
那么最终结果矩阵C中的「a*f+b*h」就能等价于 M3+M5(简直太天才了!)

于是整个传统的矩阵乘法就变成了上述的「自定义」计算模块的组合。
这些模块中虽然加(减)法次数增多了,但是乘法次数从 8 次降低到了 7 次——从 M1 到 M7 个自定义模块,每个模块只有一次乘法!
好了,现在2×2 矩阵相乘中乘法次数降低了,那么4×4 矩阵呢?
Strassen 接着说,如果一个4×4 矩阵可以划分成4 个2×2 块,那就可以用刚才的方法来处理「块矩阵」。

这下关键就来了,用Strassen 方法来做每个2×2 块的乘法(只需 7 次标量乘法),总乘法数将减少!
这样,不论是 A11、A12 和 B11 这种内部划分后的「小块」,还是外部的大块都使用Strassen 方法!
Strassen 在4×4 矩阵里不是只用一次 Strassen,而是继续对2×2 块内部再用 Strassen 方法!
Strassen再进一步递归:不是直接做 8 个2×2 矩阵乘法(每个2×2 里面是 7 次乘法),而是用「Strassen 方法组合」来只做7 次小矩阵乘法。
最终,Strassen 用两级递归做法:顶层用 Strassen 算法(做 7 次2×2 小矩阵乘法),然后每个小矩阵再用 Strassen 算法(每个小矩阵需要 7 次标量乘法),所以最后只需要7×7=49!
再次感叹,天才之作!
Strassen 将4×4 标量乘法次数从 64 降到 49,通过递归分解矩阵、使用「聪明」的加减组合,可以在保持结果正确的前提下,把原本的「傻算」乘法次数减少。
这种「减少乘法」的思路,为之后几十年更快的矩阵乘法算法打下了基础。
半个世纪以来,4×4 矩阵的最小乘法一直都是 49,再也没有新的算法出现。
但是这次,谷歌的 AlphaEvolve 在自我进化中发现了新的答案!
它是如何突破这个极限的?
上面的例子解释了,想要发现新的「算法」,你就需要找到新的「自定义」计算模块,来尽可能减少乘法运算。1969 年的Strassen 通过「人工」的方式,找到了这个解。
现在有了计算机,可以在数学上把矩阵乘法C=AB「升维」成张量线性操作的方式C=T·A·B。
这样可以构造一个三阶张量T来「描述整个矩阵乘法计算图」,在这种张量表示下,张量T告诉你如何组合A和B的元素来生成C的每一个元素。
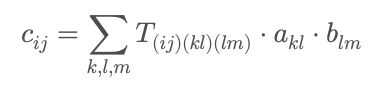
如果你能把张量T分解成如下形式,
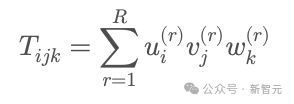
也就是把T表示为R个张量的加和(也就是)。
DeepMind 几年前就发明了 AlphaTensor 在 TensorGame 中的有限因子空间内找到张量分解。
所以整个问题就变成了:用R次乘法操作来重建整个乘法过程!
而AlphaEvolve 的任务,就是找到这个最小的R。
乘法次数「-1」
在实验中,AlphaEvolve 总共测试了 54 种不同规模的矩阵乘法问题。这些规模大致涵盖了形如⟨,,⟩的情况,其中2≤,≤5,并对做了合理的截断。
由于矩阵乘法张量本身具有对称性,对于三维轴的任意排列,存在等价的算法,因此只关注按顺序排列的规模,即≤≤。
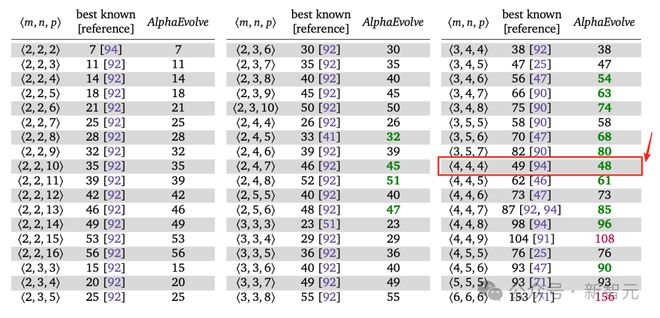
在所有情况下,AlphaEvolve 提供的都是精确算法,分解中使用的是整数或半整数的系数。
对于⟨3,4,7⟩、⟨4,4,4⟩和⟨4,4,8⟩这三种矩阵情况,AlphaEvolve 发现的算法使用了复数乘法,这些算法可用于对复数矩阵或实数矩阵进行精确乘法运算。
谷歌的研究人员说,他们当时并没有指望 AlphaEvolve 能知道比 49 次更好的方案,他们只是想要用 AlphaEvolve 来验证上述那张表格,来出个图。
(原话是:我们就是希望画这张图,用来放在论文里,显得好看)
没想到,AlphaEvolve 给了他们莫大的惊喜!
同时,谷歌提供了 AlphaEvolve 求解两个4×4 矩阵相乘所对应的三维张量的 Rank(可以简单理解为上述的乘法次数)为 48 的求解方法。



而现在,谷歌研究者的结论,已经被开发者小哥确认:AlphaEvolve 的算法的确有效!
仅用 48 次乘法,就能正确地计算4×4 矩阵的乘积,并且数值稳定性非常好,误差仅在 10^-16(机器精度)量级。
这实在是太振奋人心了。
AlphaEvolve 利用进化搜索 + LLM 引导直接在三阶张量上找到低秩分解,乘法‑加法配比为 48 次加法 +183 次乘法。
相比传统的 64 次乘法 +48 次加法,虽然加法次数变多,但是这对于计算机来讲都是小 case,只要降低乘法次数,计算效率就能指数级提升。
而和 1969 年的 Strassen 方法相比,AlphaEvolve 的乘法次数「-1」,这一枚「‑1」不仅刷新了数学纪录,更象征 AI‑for‑Science 正在成为攻克深层数学难题的新范式。
AI 突破半个世纪矩阵乘法
研究员当场惊呆
在 Youtube 采访中,我们可以看到更多细节。
就如上文所说,AlphaEvolve 打破这项纪录,连谷歌 DeepMind 的研究者都没想到。
对于通常情况下的矩阵,仍然没有比使用四十九次乘法进行两次 Strassen 更好的办法。

开始,研究者们也压根没有期待它能找到更好的结果,因为他们已经用 AlphaTensor 尝试了很长时间了。
结果,出乎所有人意料,一个更快的算法,居然被它发现了!
这次,算法使用了 48 次,而不是 49 次乘法,彻底打破纪录。
当看到一位同事发消息通知这一结果时,研究者表示自己简直不敢相信。
反复检查三遍后,他们终于确认——
AI 不断增强的能力,可以生成全新的、可证明准确的算法,从而推动科学的边界!
在专访中,当主持人问道:你可以举出一些系统做出真正有想象力的跳跃的例子吗?
研究者举的例子,就是 AlphaEvolve 发现矩阵乘法算法的过程。
实际上,他们只是让它设计了一个基于梯度的搜索算法,也即一个能找出的算法的算法,或者说元算法。
第一个搜索算法,是从一个非常简单的代码框架开始的。
研究者并未给它任何东西,只告诉它「用梯度」,然后,它就写出了这些复杂的损失函数和更新函数,而且以完全出人意料的方式引入了随机性。
就在那一刻,研究者惊呼:太厉害了!
当然,这种代码也有可能是人类写出的,但他们真的会想到写出这段特定代码吗?
那一刻,他仿佛顿悟了——AlphaEvolve 做的,是一些类似人类的事情,但又显然不是人类会尝试的东西。

而哥大的算法设计助理教授 Josh Alman 也表示,AlphaEvolve 似乎的确在产生新的想法,而不是在训练中学到的内容的重新组合。
DeepMind 研究者表示,他们有时会将一个算法的想法作为提示输入,从而产生有趣的新结果。
这就提高了人类科学家和类 AlphaZero 系统合作的可能性。
如今,AlphaEvolve 可能是人类的一小步,但已经是 AI 的一大步。
从 AlphaGo、AlphaFold 到 AlphaEvolve,下一个 Alpha,谷歌 DeepMind 还会给我们带来什么样的惊喜?
参考资料:
- http://github-phialsbasement/AlphaEvolve-MatrixMul-Verification:VerificationofGoogleDeepMind'sAlphaE
- https://www.wired.com/story/google-deepminds-ai-agent-dreams-up-algorithms-beyond-human-expertise/
- https://www.reddit.com/r/singularity/comments/1kouabz/i_verified_deepminds_latest_alphaevolve_matrix/
- https://www.youtube.com/watch?v=vC9nAosXrJw&t=2s






