
新智元报道
编辑:Aeneas 好困
给 DeepSeek-R1 推理指导,它的数学推理能力就开始暴涨。更令人吃惊是,Qwen2.5-14B 居然给出了此前从未见过的希尔伯特问题的反例!而人类为此耗费了 27 年。研究者预言:LLM 离破解 NP-hard 问题,已经又近了一步。
就在刚刚,南航、南通大学、牛津等机构的研究者发现:通过高指令的推理指令,DeepSeek-R1 有望解决数学上的 NP-hard 问题!

论文地址:https://arxiv.org/abs/2502.20545
NP-hard 问题,是计算复杂性理论中的一类问题。它们至少和 NP 问题一样难,但不一定属于 NP 类别(即不一定中多项式时间内被验证)。
本来,DeepSeek-R1、GPT-4o、OpenAI o1-mini 这些模型,是做某种数学推理难题(SoS)是很困难的,正确率也就比纯猜高一点。
但是,一旦给它们一些推理指导,所有的模型的推理能力立马噌噌上涨,专业率最高提升了 21%。
更令研究者们吃惊的是,Qwen2.5-14B-Instruct-1M 在指导下,居然用了一个新奇精巧的方法,给出了一个此前从未见过的希尔伯特问题的反例:
要知道,希尔伯特问题的反例,可并非简单推导就能得出来的。
自 1893 年问题被提出之后,首个反例的发现耗时长达 27 年!
如今,却被 LLM 短时间内破解了。
研究者们大胆预言:照这个速度演进,LLM 离破解 NP-hard 问题已经很近了。
LLM 能解决希尔伯特第十七问题吗?
如今,LLM 在众多任务上,表现已经接近人类水平,但它们在严谨数学问题求解上的能力,仍是不小的挑战。
这次,研究者决定给大模型们来一个硬核难题——判断给定的多元多项式是否为非负的。
这个问题,和希尔伯特第十七问题密切相关。后者由数学家希尔伯特在 1900 年提出后,立马成为 23 个经典数学问题之一。

而且,许多应用数学和计算数学中的关键挑战,都可以转化为判断某些多项式的非负性问题,比如控制理论、量子计算、多项式博弈、张量方法、组合优化等。
然而,判断一般多项式是否非负,是一个公认的 NP-hard 问题!
即使对于相对低阶或仅含少量变量的多项式,此问题仍然极具挑战性。
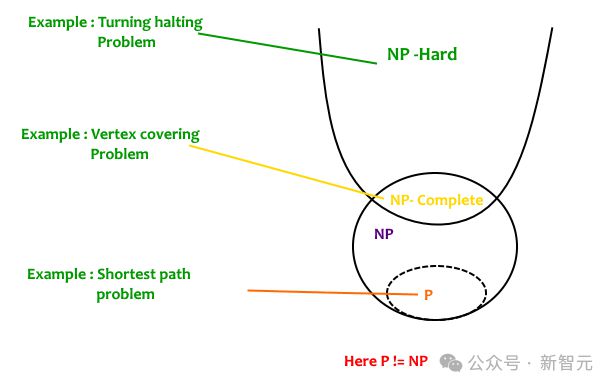
怎么办?为此,研究者们只能去寻找多项式的特殊类别,将复杂的非负性约束,替换成更简单一些的条件。
由此,平方和(SoS)条件就登场了。
作为一项数学技术,它通过将多项式表示为若干平方项的和,提供了一种充分但非必要的非负性判定方法。
所以,OpenAI o1 和 DeepSeek-R1,能解决 SoS 条件规划问题吗?
用一个数据集,给 LLM 专业推理指导
为此,研究者构建了 SoS-1K 数据集。
这个数据集经过了精心策划,包含约1,000 个多项式,并配备了五个精心设计的专家级 SoS 专业推理指导。
具体包括:
-
多项式阶数
-
主导搜索方向的非负性
-
特殊结构的识别
-
平方形式表达的评估
-
单项式的二次形式矩阵分解
接下来,属于 SOTA 模型们的考验来了!
DeepSeek-R1、DeepSeek-V3、GPT-4o、OpenAI o1-mini、Qwen2.5 系列和 QwQ-32B-Preview 在内的多位明星大模型,接受了数学难题的洗礼。
研究者们得出了一系列有趣的发现。
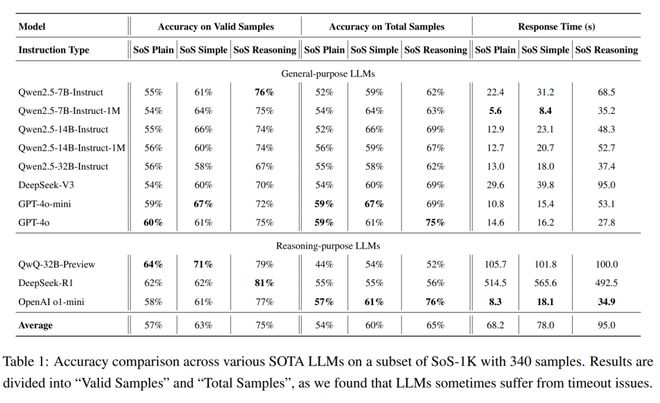
首先,如果未提供任何推理指导,所有的 SOTA 模型几乎都无法解决 SoS 问题。
它们的准确率基本都在 60%,仅仅略高于 50% 的随机猜测基线。
不过,一旦使用高质量的推理轨迹进行提示,所有模型的准确率就立马有了显著提升!
最高的提升了 21%,而且推理质量越高,模型表现就越好。
另外还有两点发现:专注于推理的 LLM 通常优于通用 LLM,无论提示质量如何。
参数较大的模型通常只用更少的推理步骤,就能正确预测,而小模型要达到最佳性能,就需要更多的推理过程了。
14B 模型竟发现了此前未见的希尔伯特问题反例
然后,研究者还进一步证明,对一个预训练的 7B 模型在 SoS1K 数据集上进行 4 小时的监督微调后,仅使用 2 张 A100 GPU,就能让它准确率从 54% 暴增至 70%,响应速度也大幅提高。
其中,SoS-7B 仅需 DeepSeek-V3 和 GPT-4o-mini 计算时间的 1.8% 和5%。
也就是说,这个 7B 模型超越了 671B 的 DeepSeek-V3 和 GPT-4o-mini 在内的更大规模模型。
然后,惊人的结果来了——
当模型被输入高质量的推理提示时,甚至在研究级问题上做出了革命性的突破。
比如,Qwen2.5-14B-Instruct-1M 就利用 Motzkin 多项式,生成了全新的、此前未见的希尔伯特第十七问题的反例。

具体来说,模型是如何发现这个反例的?
研究者展示了以下过程:通过 SoS Reasoning 提示,Qwen-14B-1M 推导出了一个新的有效 NNSoS 示例:
模型构建这个例子的方法,非常新奇有趣,令研究者赞叹不已。
它从 NNSoS 的著名例子开始,如: ,然后,引入了一个新变量并稍微修改了系数,进而生成了q_a。
这也就给了我们极大信心:按照如今 LLM 展现出的推理能力,或许有朝一日,它们真能破解 NP-hard 问题。
值得一提的是,团队只用 2 张英伟达 A100 GPU,耗时 4 小时就完成了对 Qwen2.5-7B-Instruct-1M 的微调。
由此得到的 SoS-7B 模型达到了 70% 的总体准确率,超过了 671B 参数量的 DeepSeek-V3(69%),同时响应时间仅需 1.8 秒,而 DeepSeek-V3 则需要 100 秒。
SoS-1K Dataset
首先,研究者对 SoS 多项式做出了定义。

随后,研究者们为 LLM 精心设计了指令,从而提供了结构化的分析框架,明确了约束条件,优化了逻辑推理流程,让它们显著提高了解题能力。
为此,他们构建了三种不同层次的的推理指令集。
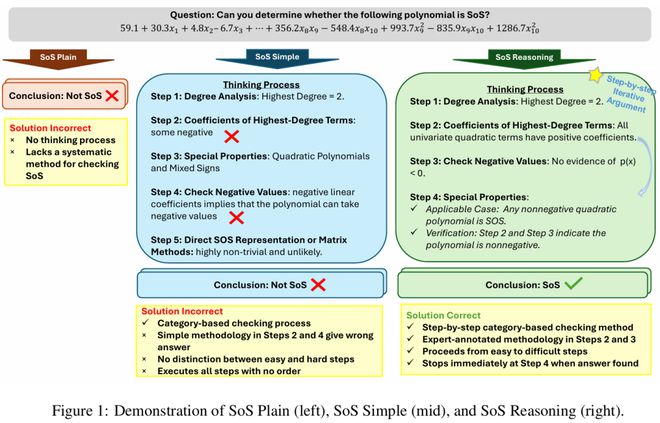
1. 基础 SoS 指令(SoS Plain)
直接向 LLM 提问:「请分析该多项式是否可以表示为平方和(SoS)」?
2. 简化 SoS 指令(SoS Simple)
将 SoS 多项式划分为五个不同类别,每个类别由简洁的一行标准定义。
3. 基于推理的完整 SoS 指令(SoS Reasoning)
这是一个结构化的五步框架,用来系统化识别 SoS 多项式。
而就是这个 SoS Reasoning,成为了 LLM 解决数学研究级问题的基础,让它们的能力扩展到更复杂的数学推理任务。
下面就是一个 SoS Reasoning 的示例。
-
步骤 1.检查次数:SoS 多项式的最高次数必须是偶数。
-
步骤 2.检查非负性:SoS 多项式对所有实数输入都应为非负值。
-
步骤 3.检查已知特例:任何非负二次多项式以及任意一元或二元的非负四次多项式均为 SoS。
-
步骤 4.检查平方形式:根据定义 2.1,SoS 多项式可表示为:p_s(x) = ∑_i{q_i(x)²}。其中,每个q_i(x)均为多项式。
-
步骤 5.检查矩阵分解:根据定理B.1,可以将多项式表示为:p(x) = y*ᵀQy*。其中,Q为对称矩阵。随后,检查Q是否为半正定矩阵。
SoS 任务上的 LLM 评估
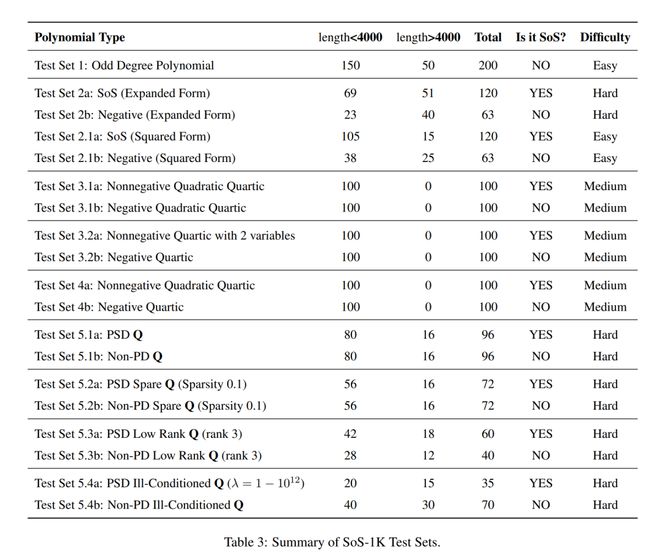
在 SoS-1K 数据集中,研究者随机抽取了约 340 道测试题,涵盖了所有测试子类别。
参与评估的有专门的推理模型(如 DeepSeek-R1、OpenAI o1-mini 和 QwQ-32B-Preview),以及通用大模型(如 DeepSeek-V3、GPT-4o 和 Qwen2.5 系列)。
结果如下。
模型对 SoS 和非负性的理解
有人可能会问:
-
模型是只学会了分类,还是真正发展出了「思考」和「构建」新证明和示例的能力?
-
当面对 SoS 或多项式优化中的研究问题时,模型能否生成具有数学意义的见解?
为了探索这一点,团队设计了一系列研究导向的问题来测试模型理解 SoS 和非负性质背后数学概念的能力。

比如,问 Qwen-7B-1M 和 Qwen14B-1M:你能提供一个文献中从未出现过的新 NNSoS 吗?
有趣的是,当使用 SoS Plain 提示时,Qwen-14B-1M 只能给出文献中已知的例子,而 Qwen-7B-1M 返回了一个不正确的答案:
虽然回答错误,但这个问题挑战性极大,即便像 YALMIP 这样的经典求解器也无法提取全局最优性。
然而,当使用 SoS Reasoning 提示向模型提出相同的研究问题时,模型正确地识别出了 pa 不是问题的有效解。
这一改进源于 SoS 推理的第 4 步,其中模型认识到p_a(x)是两个变量的非负四次多项式,因此不可能是 NNSoS。


进一步分析
Q1:模型是否遵循真正的数学逐步验证过程?
结果显示,LLM 能够按照 SoS 推理指令,一步一步生成逻辑和数学都正确的答案。
比如在下面这个例子中,o1-mini 的回复不仅在逻辑上和数学上是正确的,而且一旦模型推导出答案就自然停止,而不是盲目地遍历所有可能的步骤。



Q2:模型能否有效地从长文本多项式中提取关键信息?
与标准文本输入不同,多项式是由变量、系数、指数和项组成的复杂代数表达式。因此,对于 LLM 来说,有效解释和提取此类结构化格式中的关键信息至关重要。
分析表明,虽然 QwQ-32B-Preview 在处理超过 4K token 长度的问题时会遇到困难,但大多数 SOTA 的模型都能够成功地从 4K 长度的多项式中提取必要的系数进行评估,并生成正确的答案。
Q3:在 SoS 推理的第 1 步到第 5 步中,哪一步的准确率有所提高?
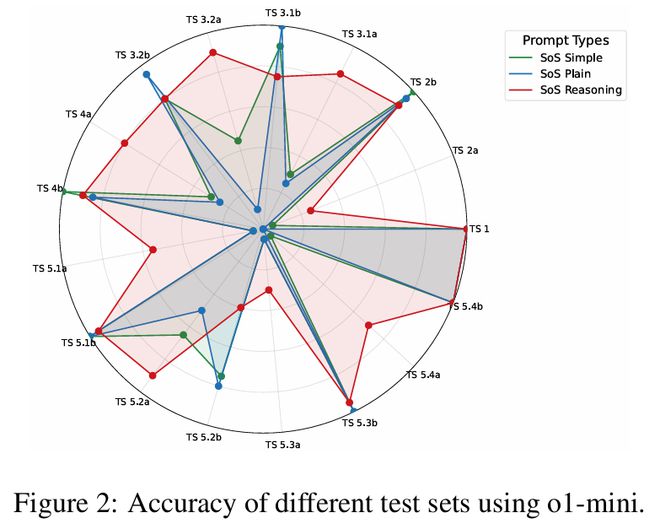
图 2 展示了 o1-mini 模型在基础 SoS(SoS Plain)、简化 SoS(SoS Simple)和完整 SoS 推理(SoS Reasoning)下不同测试集的准确率提升情况。
结果显示,最简单的 Test Set 1(对应步骤1)在所有提示方法下,都毫无意外地达到了 100% 的准确率。
得益于步骤 2 和步骤5,对于更具挑战性的 Test Sets 2a、3.1a、5.1a–5.4a,从基础 SoS 到简化 SoS 再到完整 SoS 推理,也都有持续的改进。
因为,这些步骤引入了一系列用于非负性验证的数学方法,包括常数系数检查、网格求值、首项和主导项比较、寻找最小值、矩阵分解以及寻找对称性和平移。
Q4:模型在推理过程中会「偷懒」吗?
是的,在 SoS 推理提示下观察到的另一个有趣现象是,模型在执行第 5 步时往往会「走捷径」。
具体而言,它通常会避免完全执行第 5 步中的矩阵分解或半正定规划(SDP)等复杂操作,而是基于前面步骤的结果推测答案。这种行为在处理长输入和复杂多项式时尤为普遍。
对于较简单的问题,推理模型如 o1-mini(运行时间最短,为 17 秒)和较大的模型如 QwQ-32B-Preview 往往会采取捷径,跳过第 5 步,从前面更简单的步骤中推断答案。
而 DeepSeek-V3 则不会走捷径,而是花费明显更多的时间(40 秒)正确地解决所有步骤。
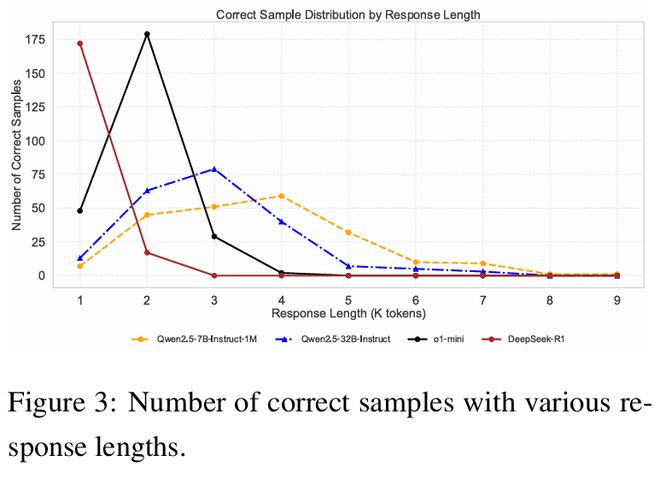
Q5:推理长度如何影响准确性?
如图 3 所示,更高性能的模型通常需要更少的思考所需 token 数量来做出正确预测,而性能较低的模型需要更多的推理步骤才行。
例如,DeepSeek-R1 和 o1-mini 在 1K-2K 的输出长度下,就达到最高的正确预测数量;而 Qwen2.5 系列需要 3K-4K 个 token 才能产生正确答案。
Q6:当前的 SOTA 模型有什么局限性?
首先,对于长输入情况,会出现无效样本。例如,在 DeepSeek-R1 中,340 个样本中只有 234 个是有效的。
其次,在处理复杂问题时,「走捷径」虽然会节省时间,但在困难步骤时过早停止并猜测答案,会对准确性产生负面影响。
第三,虽然这些模型在处理小型多项式时表现出色(准确率接近 90%),但在多项式的二次型涉及低秩矩阵分解时,表现不佳。
参考资料:






