
新智元报道
编辑:alan
近日,BitNet 系列的原班人马推出了新一代架构:BitNet a4.8,为 1 bit 大模型启用了 4 位激活值,支持 3 bit KV cache,效率再突破。
量化到 1 bit 的 LLM 还能再突破?
这次,他们对激活值下手了!
近日,BitNet 系列的原班人马推出了新一代架构:BitNet a4.8,为 1 bit 大模型启用了 4 位激活值:

论文地址:https://arxiv.org/pdf/2411.04965
众所周知,激活值量化通常是比较难办的。
本次的 BitNet a4.8 采用混合量化和稀疏化策略,来减轻异常通道引入的量化误差。
简单来说就是,对注意力层和 FFN 层的输入采用 4 位量化,同时用 8 位整数稀疏化中间状态。
大量实验表明,BitNet a4.8 在相同的训练成本下,实现了与前代 BitNet b1.58 相当的性能,同时因为可以吃到 4 位(INT4/FP4)内核的计算红利,实现了更快的推理速度。
BitNet a4.8 仅激活 55% 的参数,并支持 3 bit KV cache,进一步提升了大规模 LLM 部署和推理的效率。
BitNet a4.8
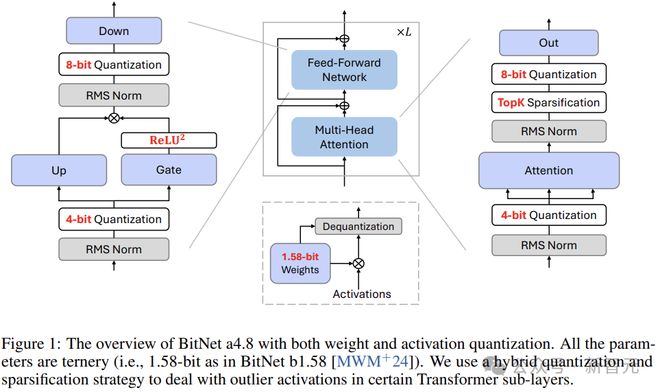
模型架构
模型的整体架构如图 1 所示,BitNet a4.8 采用了与 BitNet b1.58 相同的布局。
作者使用 BitLinear 替换注意力(MHA)和前馈网络(FFN)中的线性投影,以从头开始学习 1.58 bit 权重。对于激活值,采用混合量化和稀疏化策略来减轻异常值维度引入的误差。
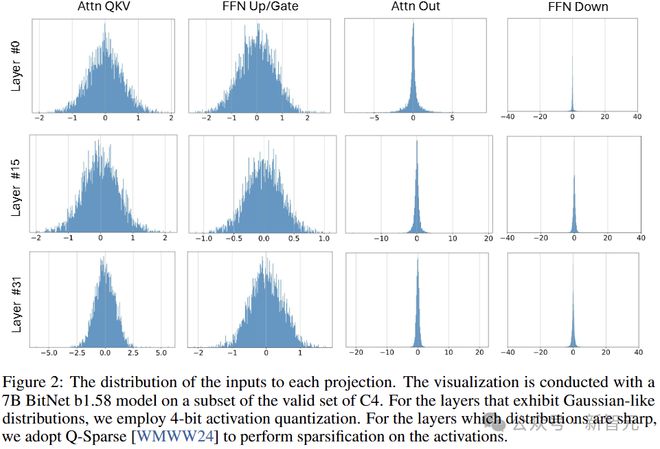
图 2 说明了模型大小为 7B 的 BitNet b1.58 中,每个模块输入的分布。
注意力层和 FFN 层的输入通常类似高斯分布,而在 FFN 下采样之前的激活值和注意力中的输出投影中,发现了很多异常值通道和大量接近零的条目(全精度 LLM 也有类似观察结果)。
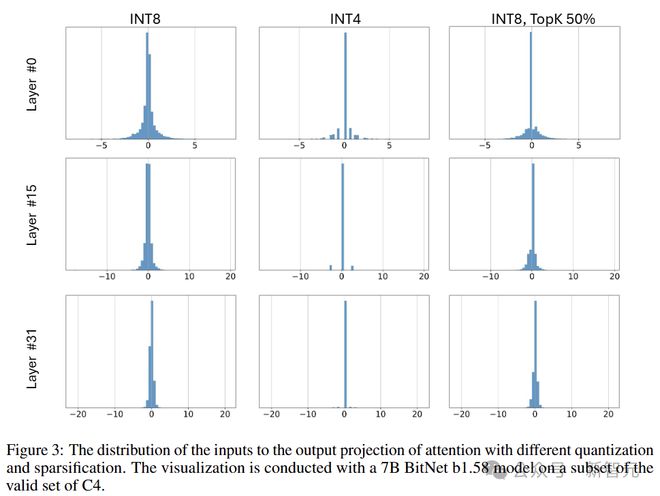
如图 3 所示,直接将低位量化应用于这些中间状态会引入很大的量化误差。
因此,作者使用Q-Sparse 的稀疏化方法,将这些中间状态保持在 8 位(同时消除了计算瓶颈)。
对于自注意层的输出投影,使用 sparsify-then-quantize 函数:
两个Q分别表示权重W和激活X的量化函数,M是掩码,根据激活X的绝对值取 topK,⊙是元素乘法。
具体来说,权重量化和激活值量化函数可以表述为:
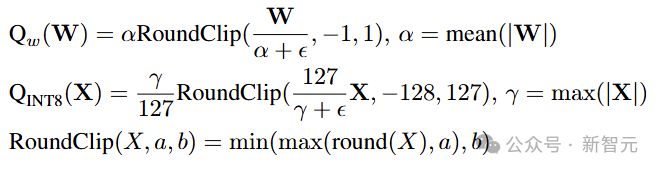
对于 FFN,这里采用 squared ReLU 和门控线性单元(GLU)来进一步提高激活的稀疏性:
根据初步实验的结果,使用 squared ReLU 时,下采样输入的稀疏性超过了 80%,且对性能的影响最小。
此外,作者还观察到 gate + squared ReLU 的输出也表现出高激活稀疏性(7B 模型为 67.5%)。通过首先计算 gate projection,然后仅在非零通道上执行 up projection,可以进一步减少推理的计算量。
相比之下,attention 和 FFN 的输入中包含的异常值特征要少得多,可以使用 absmean 函数将激活值量化为 4 位整数:

模型训练
初始化
BitNet a4.8 使用 BitNet b1.58 的权重开始训练,分为 W1.58A8 与 W1.58A4 两阶段。
第一阶段使用 8 位激活和 GLU + squared ReLU 训练模型;第二阶段采用上面介绍过的混合量化和稀疏化。

BitNet a4.8 只需少量训练,即可快速适应 4bit 位宽和稀疏激活,同时性能损失可以忽略不计。
梯度近似
作者使用直通估计器(STE)对 BitNet a4.8 进行梯度逼近,使用混合精度训练来更新参数。
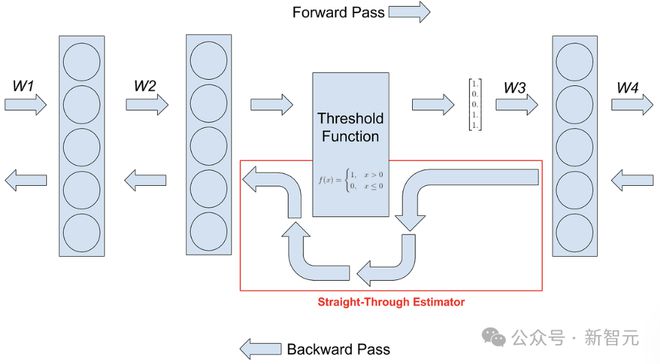
这里直接绕过了不可微函数,包括反向传播过程中的量化函数和 topK 稀疏函数。对于混合精度训练,保持全精度 latent weight 来累积参数更新。
模型量化
浮点量化提供了比基于整数的量化更宽的动态范围,这对于处理激活值的长尾分布至关重要。
研究人员将 FFN 下采样层的输入保留为 8 位整数,其他激活值使用 MinMax 量化器量化为 FP4:
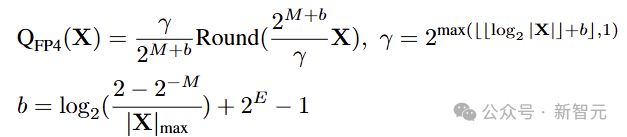
公式中E和M分别表示指数和尾数部分的位宽。这里采用 E2M1 格式,因为它的动态范围更大。
实验
本文将 BitNet a4.8、BitNet b1.58,以及各种参数量大小的 FP16 精度 LLaMA 进行了比较。
其中的 1.58 bit 模型,遵循 BitNet b1.58 的训练方案,采用了两阶段权重衰减和学习率调度。
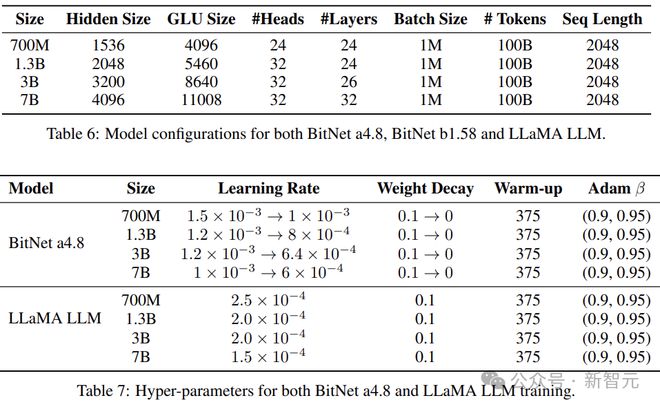
所有模型都使用 RedPajama 数据集中的 100B token 进行训练,以确保公平比较。
对于 BitNet a4.8,作者首先使用 95B token 来训练 8 位激活值的模型。然后重用优化器状态,并使用 5B token 进行混合量化和稀疏化的训练。实验将 topK 设置为 50%(attention 的输出投影位置)。
作者使用 lm-evaluation-harness 工具包,评估模型在一系列语言任务上的 zero-shot 准确性,包括 ARC-Easy(ARCe)、ARCChallenge(ARCc)、Hellaswag(HS)、Winogrande(WGe)和 PIQA(PQ)。另外还测试了在 C4 数据集(测试集)上的困惑度。
主要结果
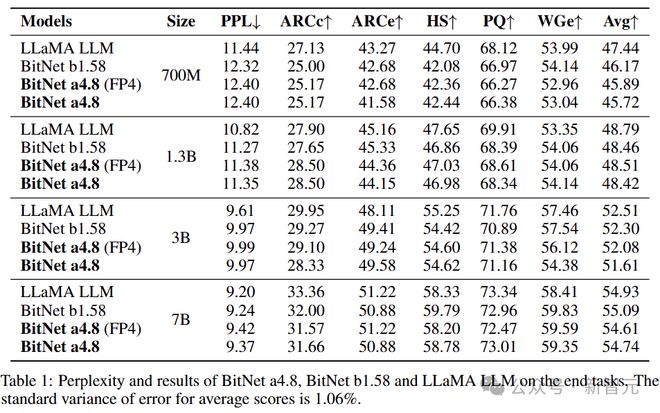
表 1 总结了 BitNet a4.8、BitNet b1.58 和 FP16 LLaMA 的详细测试结果。
全精度(FP16)LLaMA 和 BitNet b1.58 之间的性能差距,随着模型大小的增长而缩小。对于 7B 模型,BitNet b1.58 在语言模型困惑度和任务的平均准确性方面与 LLaMA 相当。
此外,相比于 BitNet b1.58,BitNet a4.8 的平均精度几乎没有损失。
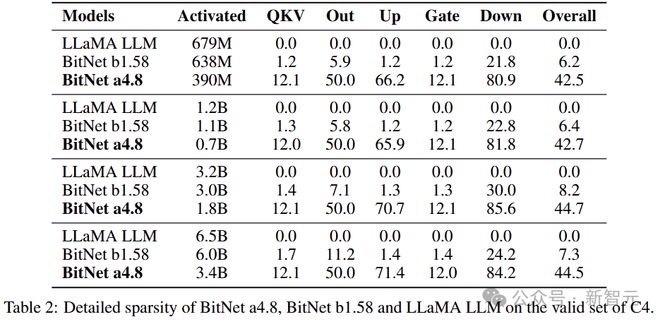
表 2 展示了各种大小的 BitNet a4.8、BitNet b1.58 和 FP16 LLaMA 中每个模块的详细稀疏性(使用 C4 验证集上的非嵌入参数计算)。
值得注意的是,BitNet a4.8 的稀疏性明显高于 BitNet b1.58 和 LLaMA。
比如在 7B 模型中,BitNet a4.8 的整体稀疏性达到了 44.5%,只有 3.4B 的活跃参数。down projection 层的输入显示出特别高的稀疏性,且中间状态分布以零为中心。
此外,gate projection 的输出非常稀疏,导致了 up projection 的高稀疏性(因为只需要在从 Gate 中选择非零通道来执行投影)。
具体来说,对于 7B BitNet a4.8,Gate 和 up projection 的稀疏率分别为 67.5% 和 12.0%。
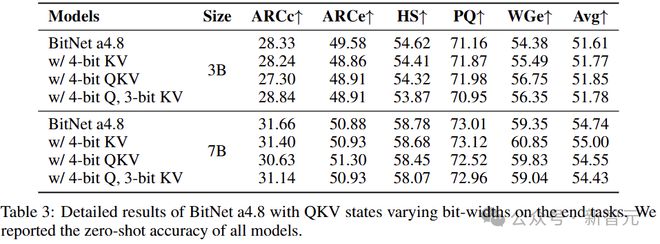
表 3 显示了 BitNet a4.8 在 3B 和 7B 模型大小下,low-bit attention 的详细情况。模型使用 4 位 KV 或 QKV 头,精度损失可忽略不计,同时 KV cache 可以量化为 3 位整数。
low-bit attention 对于高效的长序列建模至关重要,它减少了 KV cache 的内存占用和 IO,并加速了注意力计算。
在本文的实验中,作者采用 RoPE 后量化。使用 absmax 函数将 QKV 头直接量化为无符号整数,无需任何校准数据集。
对于 3 bit KV 量化,研究人员将 bos token 的头保留为 4 bit,因为它包含更多的异常值特征。
消融实验
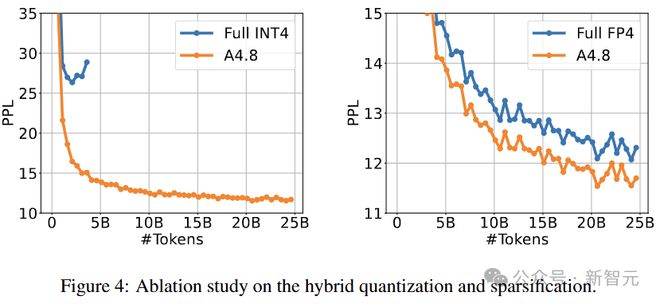
图 4 显示了 700M BitNet a4.8 的训练损耗曲线,比较了使用完整的 INT4/FP4 量化,以及本文的混合量化和稀疏化。
完整的 INT4 量化会导致发散,而混合架构在训练困惑度方面明显优于完整的 FP4 架构。
使用 RedPajama 数据集中 25B token,来进行模型的第一阶段训练,采用 absmean 和 MinMax 量化器分别进行完整的 INT4 和 FP4 量化。
对于完整的 INT4 量化,由于其输入具有更大的异常值,这里设置β = 2*mean(X)。
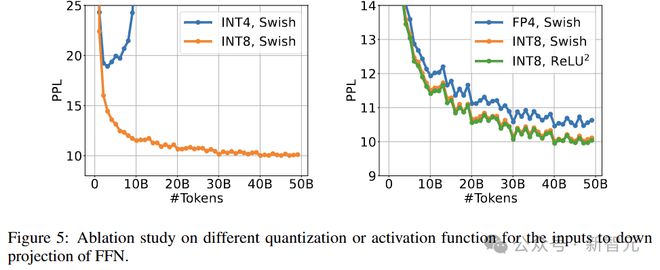
接下来为 1.3B BitNet a4.8 的 down projection 层输入,设置不同的量化或激活函数。
所有模型都使用 RedPajama 数据集中的 50B token 进行第一阶段训练。为了确保公平比较,其他激活值都保留在 8 位。
图 5 显示了这些模型的训练损失曲线。Squared ReLU 的训练困惑度比 Swish 略好,同时实现了更高的稀疏性。
此外,对 down projection 的输入应用 FP4 量化会导致性能显著下降,而将 INT4 激活与 STE 一起使用会导致发散。
参考资料:






