12. 2
知识分子
The Intellectual

图源:pixabay
撰文吴思
这篇短文不是要讨论今年诺贝尔物理学奖是否不恰当地授予了人工智能专家,而是要澄清授奖对象是否出现了重大遗漏。
John Hopfield 和 Geoffrey Hinton 两位教授获得了今年的诺贝尔物理学奖,其中 Hopfield 教授的获奖原因是因为发展了著名的 Hopfield 吸引子网络模型。由于我长期在做有点冷门的吸引子网络的理论研究(见微信公众号文章【学术思想】连续吸引子神经网络:神经信息表达的正则化网络模型),因此不少同事祝贺我,有种终于“苦尽甘来”,可以“与荣有焉”了的感觉。但我内心却是五味杂陈,因为我深知道 Hopfield 模型背后真实的故事。有朋友鼓励我说,为计算神经科学领域外的读者以及年轻学者计,我应该写下这段公案,给历史留一段记录。
简单说就是,日本著名科学家 Shun-ichi Amari(甘利俊一)教授在 1972 年就已经提出了 Hopfield 教授在 1982 年发表的 Hopfield 模型,前者比后者整整早了十年。两个数学模型几乎一模一样,而且 Amari 教授的文章还做了更深入细致的数学分析。图 1 简单对比了两个模型的最关键相同之处,包括神经元的阈值动力学(threshold dynamics)和神经元连接的 Hebbian 学习律。基于该数学模型,两篇文章都分析了网络动力学的稳定状态,即吸引子,并由此引申到了大脑的联想式记忆。读者可以仔细对比 Amari1972 年[1]和 Hopfield 1982 年[2]的文章。有科研经验的读者都知道,在模型如此相似的情况下,有了 Amari 1972 年的文章,Hopfield 1982 年的文章其实很难能发表在重要杂志上了。当然在当时资讯条件下,有可能 Hopfield 教授并不知道 Amari 教授的工作。

图1:Amari 原始模型和 Hopfield 原始模型的对比。两者的数学形式几乎是一模一样的,都采用了神经元的阈值动力学和神经元之间连接的 Hebbian 学习律。
在计算神经科学及相关领域,Amari 教授比 Hopfield 教授早十年提出 Hopfield 模型并不是一个鲜为人知的秘密,而是一个很多人都知道的事实。计算神经科学领域的著名学者 Haim Sompolinsky 教授(2023 年 Brain Prize 大奖的获得者)在一篇文章中曾评论到:“虽然 Amari 更早提出了一样的模型,但因为 Hopfield 贡献很大,所以我们叫它 Hopfield 模型“,英文参见[3]。计算神经科学领域另一位已过世的著名学者 Daniel Amit(《Modelling Brain Function: The World of Attractor Neural Networks》书的作者)曾经当面给 Amari 教授道歉,表示这是学术界的一个错误,该模型应该叫 Amari-Hopfield 模型,并赠予了 Amari 教授一条红色领带作为歉意。
诚如 Amit 教授所言,在当年资讯远远落后于今天的时代,即便是 Hopfield 教授独立发展了该模型,出于科学惯例,这个模型也应该叫 Amari-Hopfield 模型更合适。但让人费解的是,诺贝尔奖评审委员会在明知 Amari 教授早期工作的情况下(诺奖的科学背景介绍还列出了 Amari1972 年的文章),依然忽视了 Amari 教授的贡献,实在是让人难以理解。
需要申明的是,我介绍这段历史并不全因为我是 Amari 教授的弟子,有为老师发声之嫌。其实在外网的一些论坛上,对此争论更激烈。著名的德国科学家 Jurgen Schmidhurber 教授(LSTM 模型的发明人)就在一个有悠久历史的邮件群 connectionist 里为 Amari 教授的不公发声。摘录部分如下:

图2:Schmidhurber 教授对 Amari 模型早于 Hopfield 工作 10 年的评论。
可能有读者知道,Schmidhurber 教授在其它场合也为另一段公案发声,其涉及到了 Amari 教授在人工神经网络最基础的训练算法-反传算法(BackProp)上的重要贡献,我这里也介绍一下。简单说就是,Amari 教授在 1967 年就提出了 stochastic gradient descent(SGD)(但由于当时计算机算力受限,只在浅层神经网络上做了演示)[4],比 Hinton 教授等人提出的有相似思想的 BackProp(1986)[5]早了 19 年。当然我本人特别崇敬 Hinton 教授,尤其佩服他锲而不舍地把基于深度学习的人工智能技术推广到了今天的高度,但在 BackProp 的优先权上还是应该一码归一码。有好事者在 connectionist 群里发布了一张 Hinton 教授在 1997 年 ICNN 会议上介绍 BackProp 的照片,演讲题目是“What’s wrong with Backprop?”, 其中 Hinton 教授本人写下了“Amari thought it first”(见下)。
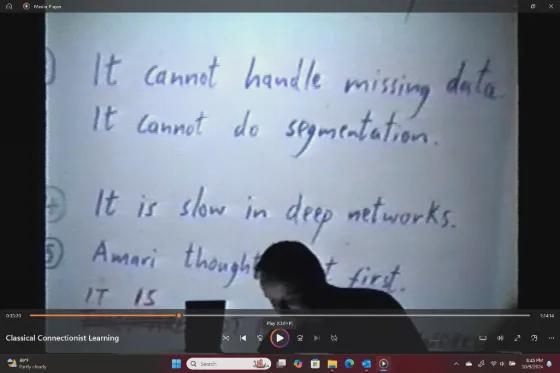
图3:Hinton 教授在 ICNN1997 会议的演讲稿,其中写下了 Amari 第一个想到 BackProp。
在诺贝尔物理学发布之后,Amari 教授很快就在日本理化学所的官网上发表了公开声明(见图4),其间只字未提自己的不公,反而真诚地祝贺了两位获奖者,体现了 Amari 教授一贯淡泊名利、与世无争的风格。但作为知情者,我认为不能因为 Amari 教授的高风亮节,我们就默认这种行为是无所谓的,其后果只会破坏科学共同体赖以健康发展的基石。
Amari 教授一生在科学上建树太多,有兴趣的读者可以参见 Amari 教授回顾其在计算神经科学领域半个世纪工作的文章[3]。除了上面提到的吸引子网络、BackProp,还有一项在我看来理论上更漂亮的工作是信息几何(information geometry)。该工作用微分几何方法分析了数据驱动的模型学习的本质,是对模型学习机理最深刻的认识。因此,我虽心有怅然,但我坚信,没有诺奖或图灵奖的加持,Amari 教授在科学上的巨大贡献也一样流芳百世!

图4:Amari 教授在诺奖结果公布后,很快就在日本理化学研究所官网上发表的公开声明(中文翻译稿)。
ZHISHI
后记
最后我也向感兴趣的读者简单介绍一下吸引子网络的后续发展。在 AI 领域,Amari-Hopfield 模型近年来被推广为了 modern Hopfield 模型[6]。在神经科学领域,Amari-Hopfield 模型逐渐被其它生物学更合理的吸引子模型代替。当前最热的吸引子网络模型是连续吸引子网络(CANN)(参见微信公众号介绍文章【学术思想】连续吸引子神经网络:神经信息表达的正则化网络模型)。特别值得指出的是,Amari 教授在 1977 年就发表一篇纯粹基于数学性质考虑的 CANN 模型[7],远远走在了实验证据的前面[8-9],也是领域内的一篇经典工作。作者在 Amari 教授实验室做博士后期间,和 Amari 教授一起发展了一个理论可解的 CANN 模型[10],并在随后的二十多年里围绕该模型开展研究。近年来,作者课题组进一步推广了该模型,在动力学方程中引入了适应性反应(adaptation),以解决吸引子网络面临的一个根本性难题:一方面,吸引子使得大脑可以稳定表征信息;但另一方面,其也不可避免地带来了副作用,即一旦神经系统进入了一个吸引子状态,就很难脱离该状态,使得大脑难以实现信息的快速迭代或搜索。通过在吸引子网络中引入时程相对较慢的适应性动力学(其可以被神经系统中广泛存在的副反馈作用实现),就能使神经系统既可以稳定地表征信息,同时又能快速搜索或迭代信息。我们系统分析该模型的计算性质[11-12],并用该模型成功了解释大量的神经生物学现象[13-14]。
本文作者吴思系北京大学心理与认知科学学院教授,麦戈文脑科学所常务副所长
参考文献:

[1]Amari, S. (1972). Learning patterns and pattern sequences by self-organizing nets of threshold elements. IEEE Transactions on Computers, C-21(11), 1197–1206.
[2]Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the United States of America, 79, 2554–2558.
[3]Amari, S. (2013). Dreaming of mathematical neuroscience for half a century. Neural Networks, 37, 48–51.
[4]Amari, S. (1967). Theory of adaptive pattern classifiers. IEEE Transactions, EC-16, 299–307.
[5]Rumelhart, D., McClelland, J., & Hinton, J. (1986). Learning internal representations by error propagation. In D. E. Rumelhart, & J. L. McClelland (Eds.), Parallel distributed processing: explorations in the microstructure of cognition, vol. 1. MIT Press.
[6]Krotov, Dmitry, and J.J. Hopfield (2016). Dense associative memory for pattern recognition. NeurIPS.
[7]Amari, S. (1977). Neural theory of association and concept-formation. Biological Cybernetics, 26, 175–185.
[8]Kim, S., Rouault, H., Druckmann, S. & Vivek Jayaraman (2017) Ring attractor dynamics in the Drosophila central brain. Science 356, 849–853.
[9]Gardner, R., Hermansen, E., Pachitariu, M., Burak, Y., Baas, N., Dunn, B., May-Britt Moser, & Moser, E. (2022). Toroidal topology of population activity in grid cells. Nature 602, 123-128.
[10]Wu, S., Amari, S. & Nakahara. H. (2002). Population Coding and Decoding in a Neural Field: A Computational Study. Neural Computation, v14, no.5, p.999-1026.
[11]Dong, X.#, Chu, T.#, Huang, T., Ji, Z.*, & Wu S* (2021). Noisy Adaptation Generates Levy Flights in Attractor Neural Networks. NeurIPS.
[12]Dong, X., Ji, Z., Chu, T., Huang, T., Zhang, W., Wu S* (2022). Adaptation Accelerating Sampling-based Bayesian Inference in Attractor Neural Networks. NeurIPS.
[13]Chu, T.#, Ji, Z.#, Zuo, J., Mi, Y., Zhang, W., Huang, T., ... & Wu, S.* (2023). Firing rate adaptation affords place cell theta sweeps, phase precession and procession. eLife.
[14]Ji, Z. L. #, Chu, T.#, Wu, S.* & Burgess, N.* (2024). A systems model of alternating theta sweepsvia firing rate adaptation. Current Biology.






