
新智元报道
编辑:编辑部 HYZ
就在刚刚,清华校友用 AI 证明了 162 个未被人类证明的数学定理,解决了 AI 无法解决陶哲轩对多项式 Freiman-Ruzsa 猜想的形式化难题!
诺贝尔物理学奖和化学奖被 AI「包圆」后,人们再次确信:基础科学研究的范式,已经被 AI 从根本上改变。
果然,就在刚刚,AI 成功证明了 162 个以前未被证明的数学定理,再次印证了这一点。

到目前为止,LLM 仍然是静态的,无法在线学习新知识,更别提证明高数定理了。
对此,来自加州理工、斯坦福和威大的研究人员提出了 LeanAgent——一个终身学习,并能证明定理的 AI 智能体。

论文地址:https://arxiv.org/abs/2410.06209
LeanAgent 会根据数学难度优化的学习轨迹课程,来提高学习策略。并且,它还有一个动态数据库,有效管理不断扩展的数学知识。
值得一提的是,整个学习过程中,它既能自我学习新知识,同时不会遗忘已具备的能力。
实验结果发现,LeanAgent 从来自 23 个不同 Lean 代码库中,成功证明 162 个此前未被人类证明的数学定理。
相较于基于 Lean 数据微调大模型,LeanAgent 性能直接飙升 11 倍。而且,综合终身学习能力近 94%。
其中,有许多是高等数学定理,比如具有挑战性的抽象代数、代数拓扑。
它还展现出了从基本概念到高级主题清晰的学习过程。
同时,LeanAgent 在稳定性、反向迁移方面取得了卓越的成绩,并且学习新任务还能提高以往任务的性能。
陶哲轩的证明,AI 依然无解?
交互式定理证明器(ITPs),如 Lean,已成为形式化和验证数学证明的工具。
然而,使用 ITPs 构建形式化证明不仅复杂,且非常耗时。因为它需要极其详细的证明步骤,并需要使用大量数学代码库。
诸如 o1、Claude 先进的大模型,在非形式化证明中,会产生幻觉。这愈加凸显了,LLM 在形式化数学证明中准确性、可靠性方面的重要性。
先前的一系列研究,探索了 LLM 也能够生成完整的证明步骤。
比如,LeanDojo 便是基于开源大模型构建的定理证明器。研究人员通过在特定数据集上,训练微调大模型而来。

然而,形式化定理证明数据非常稀缺,进而阻碍了这一方法的泛化能力。
再比如,ReProver 专门针对 Lean 定理证明代码库 mathlib4 微调的大模型。尽管这个数据库包含了超 10 万个形式化数学定理、定义,但它们分布仅覆盖的是本科数学。
因此,ReProver 在更具挑战性问题——陶哲轩对多项式 Freiman-Ruzsa(PFR)猜想的形式化,表现就会很差。

https://terrytao.wordpress.com/2023/11/13/on-a-conjecture-of-marton/
并且,数学研究动态性,更是加剧了无法泛化的问题。
数学家们通常同时,或者交替在多个领域、项目中进行形式化。
比如,陶哲轩并行开启多个项目,包括 PFR 猜想、实数对称平均、经典牛顿不等式、渐近分析的形式化。
Patrick Massot 专注于形式化 Scholze 凝聚态数学,以及完美空间(Perfectoid Spaces)项目。

这些例子突出了当前 AI 定理证明方法一个关键不足:
缺乏一个能够随时间在不同数学领域自适应、改进的 AI 系统,特别是在 Lean 数据可用性有限的前提下。
与终身学习的相关性
至关重要的是,数学家们形式化过程与终身学习密切相关,即在不忘记的情况下学习多个任务。
然而,对于 AI 来说,一个重大挑战便是「灾难性遗忘」问题。
它们往往会学习新知识(新分布)后,直接丢失,甚至抹去了对旧知识(旧分布)的记忆。
而核心挑战是,如何去平衡可塑性(学习和适应的能力)与稳定性(保留现有知识的能力)。
当 AI 学习新任务时,可能会覆盖了先前的学习信息。而若是为了增强稳定,保留既有的知识,便会损害 LLM 获取新技能的能力。
在数学形式化定理证明中,AI 持续泛化能力的关键,便是在这两者之间实现平衡。
LeanAgent:首个终身学习证明数学定理的 AI 智能体
基于以上难题,LeanDojo 原班人马团队提出了 LeanAgent,一个用于定理证明的全新终身学习框架。
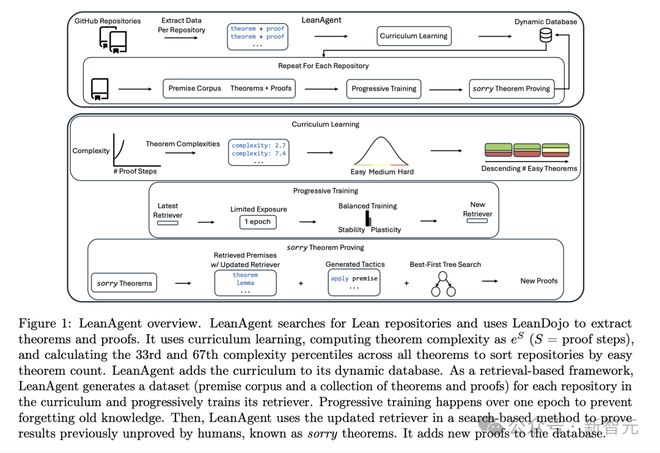
如下图 1 所示,LeanAgent 工作流包括了:
-
推导定理的复杂度,以计算学习课程
-
进行渐进训练,在学习过程中平衡稳定性和可塑性
-
利用最佳优先树搜索,来搜索 sorry 定理(人类尚未证明的定理)
当然,LeanAgent 可与任何 LLM 结合使用,并且通过「检索」来提高泛化能力。
同时,LeanAgent 包含了几个关键的创新——
使用自定义动态数据库,管理不断扩展的数学知识;使用一种新颖课程学习(curriculum learning)策略,利用 Lean 证明结构,来学习更复杂的数学仓库。
对于 AI 灾难性遗忘问题,研究人员采用了简单的「渐进」训练方法。
该方法让 LeanAgent 能够持续适应新的数学知识,同时还能保留先前的学习信息。
这一过程涉及了,在课程中每个仓库生成的新数据集上,增量训练检索器。
从预训练检索器开始(比如基于 ByT5 ReProver 检索器),LeanAgent 在每个新数据集上,额外训练一个 epoch。
通过将渐进训练限制在一个 epoch,有助于平衡稳定性和可塑性。
尤其是,渐进训练对数据库生成的每个数据集重复进行,逐步扩展 LeanAgent 知识库。
它的优势是,增加了可能的证明状态空间(其中状态包括定理的假设和当前证明进展),同时向前提嵌入添加了新的前提。
不过,更复杂的终身学习方法,如弹性权重合并(EWC),使用 Fisher 信息矩阵来约束先前任务的重要权重,会导致过度可塑性。
这种不受控制的可塑性,是因为 AI 无法随着定理复杂度的增加,而适应参数重要性。
它迫使 AI 在学习高级概念时,关键参数会发生快速变化。
因此,这些方法是无法适应数学定理不断演变复杂性,也就无法适用在定理证明中的终身学习。
如前所述,在 23 个不同的 Lean 代码库中, LeanAgent 在定理证明终身学习方面取得了优越性。
它成功证明了 162 个 sorry 定理,其中许多来自高等数学。
比如,LeanAgent 证明了来自 PFR 仓库的困难 sorry 定理,并证明了抽象代数和代数拓扑中与 Coxeter 系统和毛球定理相关的挑战性定理。
另外,研究人员还发现,LeanAgent 在定理证明中,展现出渐进学习的一面。
从最初证明基本的 sorry 定理,到后面证明了更复杂的定理。
而且,LeanAgent 在只能证明新的 sorry 定理方面,比静态 ReProver 基线高出多达 11 倍,同时保留了对已知定理证明的能力。
在定理证明中,作者还发现稳定性(在不失去太多可塑性前提下),对于 AI 持续泛化到新仓库至关重要。
反向迁移(BWT),即学习新任务改善先前学习任务的性能,也在定理证明中至关重要。
数学家需要一个既能持续泛化,又能持续改进的定理证明终身学习框架。
最后的消融实验中,相较于 7 个终身学习框架,LeanAgent 简单的课程学习和渐进训练组件,显著提高了稳定性和 BWT 得分。
最终,LeanAgent 拿下了 94% 综合终身学习的成绩,几乎接近完美。
这也揭示了,LeanAgent 在持续泛化和改进的强大能力,以及卓越的 sorry 定理证明性能。
LeanAgent 对数学知识的掌握
在终身学习过程中,LeanAgent 展示了对基本代数结构和基本数学运算的深刻理解。
a)群和环论
LeanAgent 证明了关于基本代数结构的定理。例如,MyGroup.mul_right_inv 证明了将一个元素与其逆元素相乘等于单位元,而 MyRing.add_right_cancel 则展示了环加法的消去性质。
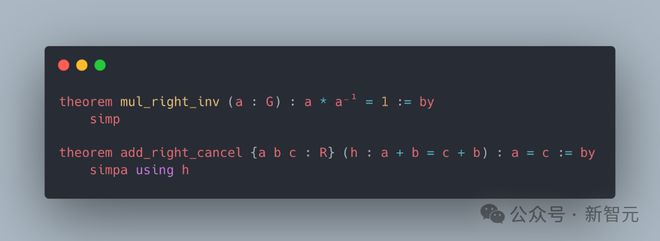
b)初等数论
LeanAgent 可以处理基本的算术属性。例如,MyRing.zero_mul 证明了零乘以任何数都是零,而 MyRing.neg_neg 则证明了负数的负数等于原数。
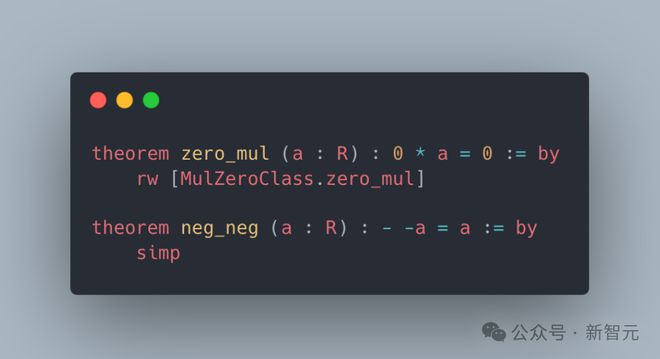
c)序理论
LeanAgent 掌握了序理论的相关概念。例如,absorb 1 证明了x与(x和y的上确界)的下确界总是等于x,而 absorb2 证明了x与(x和y的下确界)的上确界总是等于x。
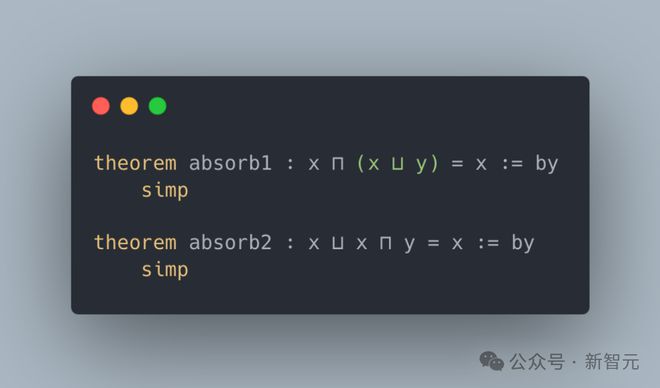
d)初等实分析
LeanAgent 展示了对实数及其绝对值性质的初步理解。例如,C03S05.MyAbs.abs_add 证明了涉及实数的三角不等式。
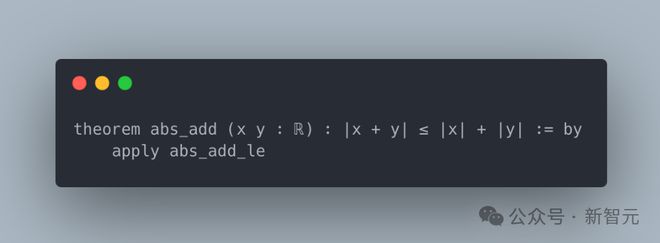
终身学习过程表明,LeanAgent 已经从基础开始理解数学概念。而在这个过程结束后,它的数学推理能力有显著提升。
比如证明了涉及多个量词和条件的边界和绝对值的复杂命题。

理解了抽象集合论的概念,证明了子集关系是传递的。
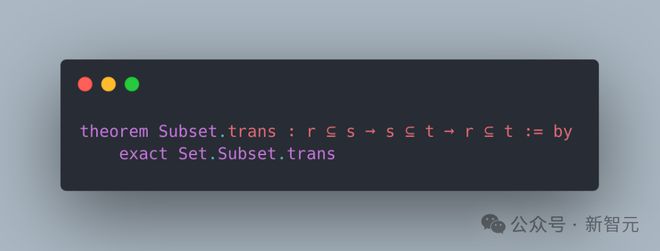
方法
用于定理证明的有效终身学习策略,需要(a)最佳仓库顺序策略和(b)最佳学习策略。
通过课程学习,研究者解决了(a),以利用 Lean 证明的结构,并通过渐进式训练来解决(b),以平衡稳定性和可塑性。
LeanAgent 由四个主要组件组成:课程学习、动态数据库管理、检索器的渐进式训练和 sorry 定理证明。
课程学习
LeanAgent 采用课程学习方法,学习逐渐增加复杂度的数学代码库。
这个过程优化了 LeanAgent 的学习轨迹,让它能够在处理更高级的概念之前,先建立坚实的基础知识。
具体步骤如下:
-
自动搜索并克隆 GitHub 上的 Lean 代码库。
-
使用 LeanDojo 提取每个代码库中定理、证明和依赖关系的细粒度信息。
-
使用公式 eS 计算每个定理的复杂度,其中S代表证明步骤的数量。对于没有证明的 sorry 定理(即未完成证明的定理),赋予无限复杂度。
-
采用指数缩放,来解决随着证明长度增加可能出现的证明路径组合爆炸问题。
-
计算所有代码库中所有定理复杂度的第 33 百分位和第 67 百分位。
-
将非 sorry 定理分为三组:简单(复杂度低于第 33 百分位)、中等(复杂度在第 33 百分位和第 67 百分位之间)和困难(复杂度高于第 67 百分位)。
-
按照代码库中包含的简单定理数量对代码库进行排序,形成课程基础。
LeanAgent 从包含最多简单定理的代码库开始学习。
动态数据库管理
在建立课程后,研究者进行以下操作:
-
将排序后的代码库添加到 LeanAgent 的自定义动态数据库中,使用 LeanAgent 提取的数据。
-
将每个定理的复杂度包含在动态数据库中,以便未来课程中高效重用代码库。
-
对课程中的每个代码库,LeanAgent 使用动态数据库生成数据集,遵循与制作 LeanDojo 基准测试 4 相同的程序。
生成的数据集包括:
-
一系列定理及其证明
-
每个证明步骤的详细注释,说明该步骤如何改变证明的状态
-
定理状态信息,包括假设和证明进展
-
展示如何按顺序使用特定的策略(函数)和前提来证明定理
-
前提语料库,作为事实和定义的参考库
检索模型的渐进式训练
LeanAgent 在新生成的数据集上,对其检索模型进行渐进式训练。
这种策略使 LeanAgent 能够持续适应新数据集中前提的新数学知识,同时保留先前学习的信息,这对定理证明的终身学习至关重要。
渐进式训练通过逐步整合每个代码库的新知识来实现这一目标。训练过程如下:
-
起点选择:虽然 LeanAgent 可以与任何 LLM 配合使用,但研究者选择从 ReProver 的检索模型开始。这是 ByT5 编码器的微调版本,利用其从 mathlib4 获得的一般预训练知识。
-
新数据集训练:在新数据集上额外训练 LeanAgent 一个 epoch(训练周期)。这种有限的训练有助于防止对新数据过拟合,同时允许 LeanAgent 学习重要的新信息。
-
嵌入预计算:在验证之前,预先计算语料库中所有前提的嵌入,以确保这些嵌入与 LeanAgent 的当前状态一致。
-
模型评估:
- 计算可塑性:保存在前十个检索到的前提(R@10)的验证召回率最高的模型迭代。这是一个原始可塑性值,用于评估 LeanAgent 适应新数学类型的能力。
- 计算稳定性:计算模型在所有先前渐进式训练过的数据集上的平均测试R@10,作为原始稳定性值。
-
重复过程:对从数据库生成的每个数据集重复上述步骤,体现训练的渐进性质。
渐进式训练的效果:
-
将新的前提添加到前提嵌入中
-
增加可能的证明状态空间
-
使 LeanAgent 能够探索更多样化的证明路径
-
发现无法用原始知识库产生的新证明
sorry 定理的证明
对于每个 sorry 定理,LeanAgent AI 智能体会通过最佳优先树搜索生成证明。具体步骤如下:
1. 前提检索:
-
使用之前收集的整个前提语料库的嵌入
-
基于当前证明状态(表示为上下文嵌入)与前提的相似性,从前提语料库中检索相关前提
-
使用语料库依赖图进行过滤,确保只考虑当前文件可访问的前提
2. 策略生成:
-
将检索到的前提添加到当前状态
-
使用束搜索生成策略候选
3. 状态评估:
-
将每个策略候选通过 Lean 运行,获得潜在的下一个状态
-
每个成功的策略应用都会向证明搜索树添加一条新边
4. 策略选择:
-
选择具有最大累积对数概率的策略,即导致该状态的策略序列的累积对数概率
5. 回溯处理:
-
如果搜索遇到无效路径,进行回溯并探索替代路径
6. 迭代过程:
-
重复上述步骤,直到满足以下条件之一:a) 找到证明 b) 穷尽所有可能性 c) 达到 10 分钟的时间限制
7. 结果处理:
-
如果 LeanAgent 找到证明,将其添加到动态数据库中
-
新证明中添加的前提将包含在涉及当前代码库的未来前提语料库中
-
LeanAgent 可以在未来的渐进式训练中从新证明中学习,进一步改进其性能
如前所述,研究者对从数据库生成的每个数据集重复这个过程,因此这种训练具有渐进性质。
渐进式训练将新的前提添加到前提嵌入中,并增加了可能的证明状态空间。
这使 LeanAgent 能够探索更多样化的路径来证明定理,发现它无法用原始知识库产生的新证明。
实验
sorry 定理的证明
研究者比较 LeanAgent AI 智能体在持续学习过程中和之后能够证明的 sorry 定理,并与 ReProver 基准进行对比。
选择 ReProver 作为基准,是因为在实验中使用了它的检索器作为 LeanAgent 的初始检索器。
然而,由于定理证明难度的非线性特性,研究者避免在 LeanAgent 和 ReProver 之间进行简单的百分比比较。
值得注意的是,LeanAgent 在多个代码库中显著优于基准的性能,让它能够证明越来越难的定理。
此外,sorry 定理缺乏已知的证明,因此证明一个 sorry 定理,对数学研究具有重要价值。
基于以上考虑,研究者提出了一个定理证明性能得分(Theorem Proving Performance Score,TPPS),特别强调新证明的 sorry 定理。
TPPS 的计算方法如下:
-
LeanAgent TPPS = (# ReProver Theorems Proved) + (# New Theorems Proved * X) + 1
-
ReProver TPPS = (# ReProver Theorems Proved) + 1
-
improvement Factor = (LeanAgent TPPS) / (ReProver TPPS)
其中,X代表证明新定理的重要性权重。考虑到基础算术和抽象代数之间的巨大难度差距,研究者选择了 X = 10。
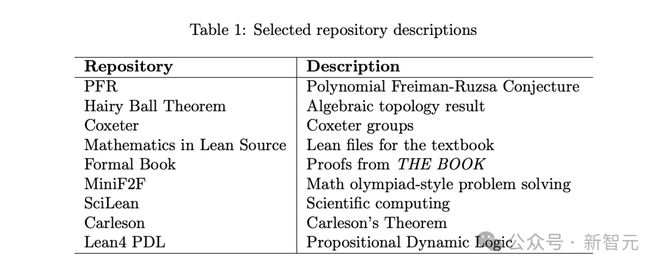
此外,LeanAgent AI 智能体的一个使用场景,是在学习完一个课程后在新的代码库中进行形式化(即将数学概念和证明转化为计算机可验证的形式)。
研究者通过在 MiniF2F 上逐步训练来展示这一点。需要注意的是,我们选择了 MiniF2F 代码库的 Lean4 版本,并忽略了其验证集和测试集的划分(原因详见附录A.5)。
数学家可以使用 LeanAgent 进行以下两步操作:
1. 学习初始课程A
2. 学习子课程B
然后,LeanAgent 可以帮助数学家并行地形式化课程A+B中的代码库。
为了演示这种情况,研究者在 8 个代码库组成的子课程B上继续训练 LeanAgent。结果见表2,案例研究见图2。
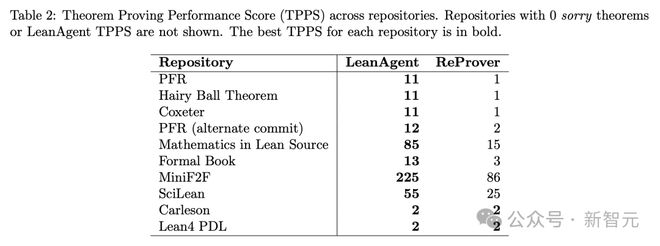
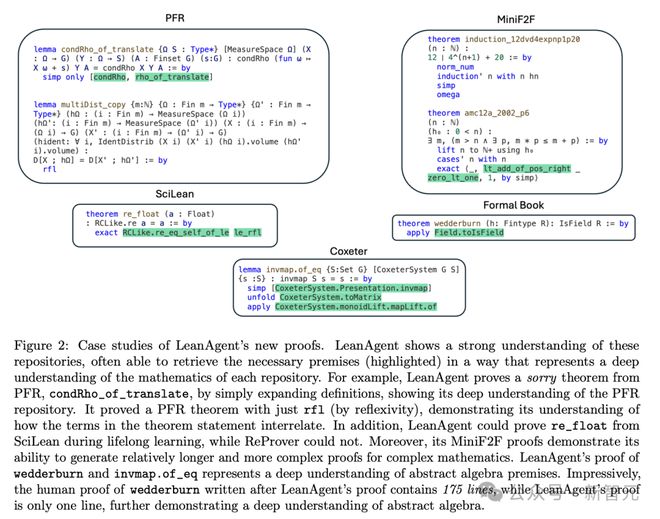
LeanAgent 在多个代码库中,展示了持续的泛化能力和定理证明能力的提升。
在终身学习结束时,LeanAgent 相比 ReProver 的改进因子如下:
- PFR:11 倍
- Mathematics in Lean Source:5.67 倍
- MiniF2F:2.63 倍
- SciLean:2.2 倍
- Hairy Ball 定理:11 倍
- Coxeter:11 倍
- Formal Book:4.33 倍
在大多数情况下,LeanAgent 的证明是 ReProver 所证明的 sorry 定理的超集。LeanAgent 的学习进展从基本概念(如算术、简单代数)逐步深入到高级主题(如抽象代数、拓扑学)。
1. PFR:
LeanAgent AI 智能体能够证明这个前沿代码库中的一个 sorry 定理,而 ReProver 做不到。它还能泛化到不同的代码提交,仅使用 rfl 策略就能证明 ReProver 无法证明的定理。有趣的是,LeanAgent 对 PFR 代码库中的逻辑操作理解得足够深入,能够用「0 = 1」这样的占位符定理语句,证明 5 个 sorry 定理。
2. SciLean:
在终身学习过程中,LeanAgent 证明了与基本代数结构、线性和仿射映射以及测度论基础相关的定理。到终身学习结束时,它掌握了高级函数空间、复杂双射和抽象代数结构的概念。
3. Mathematics in Lean Source:
在终身学习过程中,LeanAgent 证明了关于基本代数结构和基本算术性质的定理。到终身学习结束时,它能够证明涉及量词操作、集合论和关系的复杂定理。
4. MiniF2F:
ReProver 展示了在基础算术、初等代数和简单微积分方面的熟练程度。然而,到终身学习结束时,LeanAgent 掌握了高级数论、复杂代数、复杂微积分和分析、抽象代数以及复杂归纳法。
5. 子课程:
-
Formal Book 代码库:LeanAgent 从证明基本实分析和数论定理进步到掌握高级抽象代数,其证明 Wedderburn 小定理就是一个例证。
-
Coxeter 代码库:LeanAgent 证明了一个关于 Coxeter 系统的复杂引理,展示了它在群论方面的熟练程度。
-
Hairy Ball 定理代码库:LeanAgent 证明了该定理的一个关键步骤,展示了对代数拓扑的理解。
LeanAgent 能够证明这些令人印象深刻的定理,表明它比 ReProver 具有更高级的定理证明能力。
终身学习分析
因为文献中不存在其他用于定理证明的终身学习框架,因此研究者进行了一项消融研究,使用七个终身学习指标,来展示 LeanAgent AI 智能体在处理稳定性-可塑性权衡方面的优越性。
这些结果有助于解释 LeanAgent AI 智能体在 sorry 定理证明性能方面的优势。
研究者为原始的 14 个代码库课程计算了这些指标。
具体来说,消融研究包括七个额外的设置,这些设置由学习和数据集选项组合而成。学习设置的选项是有或没有 EWC 的渐进式训练。
数据集设置涉及数据集顺序和构建。数据集顺序的选项包括单一代码库或合并所有,其中每个数据集由所有先前的代码库和新的代码库组成。
考虑到 GitHub 上按星级计数最受欢迎的代码库,数据集构建的选项包括受欢迎度顺序或课程顺序。
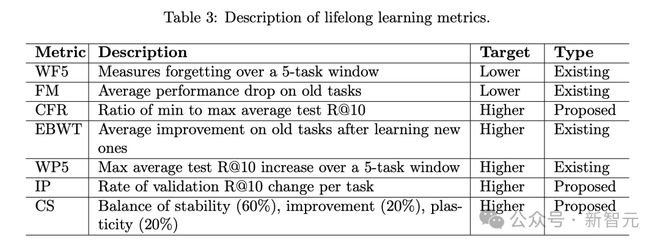
研究者使用了以下七个终身学习指标:
1. 窗口遗忘5(WF5)
2. 遗忘度量(FM)
3. 灾难性遗忘恢复力(CFR)
4. 扩展反向迁移(EBWT)
5. 窗口可塑性5(WP5)
6. 增量可塑性(IP)
7. 综合得分(CS)
他们引入了三个新指标,来解决定理证明中终身学习的特定方面:
-
灾难性遗忘恢复力(CFR):这个指标捕捉了 LeanAgent AI 智能体在其最弱任务上,相对于其最佳表现保持性能的能力,这在存在多样化数学领域的情况下至关重要。
-
增量可塑性(IP):IP 提供了比总体措施更细粒度的可塑性视图,并对任务顺序敏感,这在定理证明的终身学习中特别相关。
-
综合得分:目前应该还没有广泛建立的综合指标能够提供一个单一的稳定性-可塑性权衡得分,包含表 3 中的前六个指标。
因此,研究者提出了一个综合得分:Composite Score = 0.2 · (1 − WF5_norm) + 0.2 · (1 − FM_norm) + 0.1 · WP5_norm + 0.1 · IP_norm + 0.2 · EBWT_norm + 0.2 · CFR_ norm
此外,这些指标在合并所有策略中衡量的是累积知识改进而不是孤立的任务表现。

1. 单一代码库分析
表 4 呈现了,单一代码库的结果。
LeanAgent 智能体在多项指标上,展现出卓越的稳定性。其 WF5 指标比下一个最佳设置低 75.34%,表明它能更有效地在一个时间窗口内保持性能。
LeanAgent FM 得分比设置 3 还要低 59.97%,展示了其对灾难性遗忘的强大抵抗力。
此外,LeanAgent 智能体、设置 1 和设置 2 中,都表现出高度一致的不会出现灾难性遗忘,CFR 值均超过 0.87,差异极小(仅±0.01)。
这恰恰凸显了,LeanAgent 智能体随时间持续泛化的能力。
另外,它 EBWT 高出 16.25%,进而表明其具备了随时间持续改进的能力。
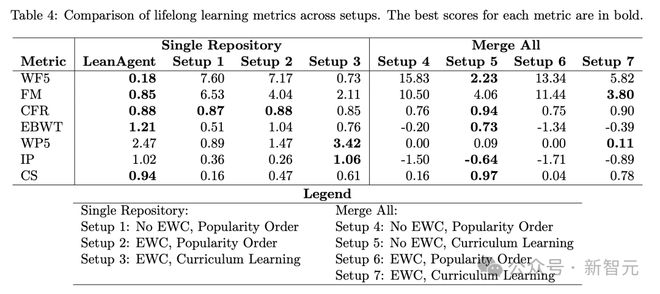
相比之下,设置 3 表现出更高可塑性。
它的 WP5 比 LeanAgent AI 智能体高出 38.26%,表明其在一个时间窗口内,快速适应新任务的能力更强。
设置 3 IP 比 LeanAgent 智能体高出 3.98% 相辅相成,暗示了随着时间推移,其在新任务上改进更为显著。
然而,这些可塑性的提升是以极大代价换来的:设置 3 产生了更严重的灾难性遗忘,可从其与 LeanAgent 智能体相比明显较差的稳定性指标可以看出。
设置 3 中过度的可塑性,源于 EWC 无法随定理复杂性增加而调整参数重要性。
EWC 保留了对简单定理重要的参数,但这些参数可能对更复杂的定理,并不关键。
因此,这些保留的参数抗拒变化,而其他参数为复杂定理快速变化。这迫使模型整体变得更具可塑性,在处理新的复杂定理时严重依赖非保留参数。
LeanAgent AI 智能体在综合得分上表现出卓越性能,能够在适应新任务的同时,保持已有知识,使其成为单一代码库设置中最适合终身学习智能体。
2. 合并所有分析
接下来,研究人员分析了表 4 中的合并所有设置。
设置 5 的 WF5 指标比下一个最佳设置(设置7)低 61.68%,表明设置 5 在不断扩大的数据集中最有效地实现可塑性和稳定性平衡。
此外,设置 5 的 CFR 得分比设置 7 高 3.77%,再次展示了面对不断扩大、可能更复杂的数据集时的高度且一致的抵抗力。
然而,设置 7 的 FM 得分比设置 5 低 6.44%,展示了其在早期数据点上能够保持已有知识的能力。
此外,设置 5 是唯一一个 EBWT 为正的设置,表明学习新任务可以提高整个历史数据集的性能。其他设置的 EBWT 为负,表明在学习新任务后,早期任务的性能有所下降。
只有设置 5 和 7 的 WP5 不为0,表明它们有能力适应合并数据集不断增加的复杂性。
设置 4 和 6 为 0 数值表明,在处理合并数据时,按受欢迎程度排序难以显示改进。然而,尽管设置 5 的 IP 得分最高,比设置 7 高 27.75%,但所有 4 个设置的 IP 值都为负。
这表明验证R@10 随时间推移而下降,说明合并所有策略难以保持性能。
设置 5 的高综合得分表明,它在平衡保留早期知识与适应合并数据集中的新数据方面表现最佳。然而,其负 IP 值表明其方法存在根本性问题。
3. 比较分析和洞见
尽管这些指标在单一代码库和合并所有设置中有不同的解释,但研究者表示,仍然可以通过关注整体趋势和相对表现,来进行一些有意义的比较。
研究者注意到,合并所有设置中的负 IP 值表明存在重大问题。
这个缺点超过了其他指标所显示的潜在优势,因为它揭示了在持续增长的数据集中无法保持和改善性能的根本问题。
相比之下,LeanAgent 展示了正 IP 值,表明其能够有效吸收新知识。
这一特点,再加上其相对于其他单一代码库方法更优越的稳定性和 EBWT 指标,表明 LeanAgent 比设置 5 更适合实现持续的泛化能力和性能改进。
4. 与 sorry 定理证明性能的一致性
这种终身学习分析与 LeanAgent 在 sorry 定理证明方面的性能表现是一致的。
LeanAgent 优越的稳定性指标(WF5、FM 和 CFR),解释了它在不同数学领域保持性能的能力,这一点从它成功证明来自 SciLean、Mathematics in Lean Source 和 PFR 等不同代码库的定理中就可以被证实。
其高 EBWT 分数与它在定理证明中从基本概念到高级主题的进展相一致。
虽然 LeanAgent 相比某些设置显示出略低的可塑性(WP5 和 IP),但这种权衡实际上导致了更好的整体性能。这一点体现在它能够证明比其他方法更广泛的 sorry 定理集合。
由持续泛化能力、持续改进和可塑性组成的综合得分,进一步证实了 LeanAgent 在定理证明的终身学习方面具有全面的优势。
作者介绍
Peiyang Song

Peiyang Song 是加州理工学院(Caltech)计算机科学的本科生,由 Steven Low 教授的指导。同时也是斯坦福人工智能实验室(SAIL)的研究员,在计算与认知实验室(CoCoLab)由 Noah Goodman 教授指导。
他的研究方向是机器推理,特别是用于数学和代码生成的 AI。此前,从事过高能效机器学习系统和机器翻译的研究。
Chaowei Xiao

Chaowei Xiao 是威斯康星大学麦迪逊分校的助理教授,同时也是英伟达的研究员。
他的研究方向是探索 LLM 系统的安全性和安全保障,以及 LLM 在不同应用领域中的作用。
此前,他在密歇根大学安娜堡分校获得博士学位,并在清华大学获得学士学位。
参考资料:






