
新智元报道
编辑:桃子
KAN 的诞生,开启了机器学习的新纪元!而这背后,竟是 MIT 华人科学家最先提出的实践想法。从 KAN 到 KAN 2.0,这个替代 MLP 全新架构正在打开神经网络的黑盒,为下一步科学发现打开速通之门。
KAN 的横空出世,彻底改变了神经网络研究范式!
神经网络是目前 AI 领域最强大的工具。当我们将其扩展到更大的数据集时,没有什么能够与之竞争。
圆周理论物理研究所研究员 Sebastian Wetzel,对神经网络给予了高度的评价。

然而,万事万物并非「绝对存在」,神经网络一直有一个劣势。
其中一个基本组件——多层感知器(MLP),尽管立了大功,但这些建立在 MLP 之上的神经网络,却成为了「黑盒」。
因为,人们根本无法解释,其中运作的原理。
为此,AI 界的研究人员们一直在想,是否存在不同类型的神经网络,能够以更透明的方式,同样输出可靠的结果?
是的,的确存在。
2024 年 4 月,MIT、加州理工等机构研究人员联手提出,新一代神经网络架构——Kolmogorov-Arnold network(KAN)。
它的出现,解决了以上的「黑盒」问题。

论文地址:https://arxiv.org/pdf/2404.19756
比起 MLP,KAN 架构更加透明,而且几乎可以完成普通神经网络,在处理某类问题时的所有工作。
值得一提的是,它的诞生源于上个世纪中期一个数学思想。

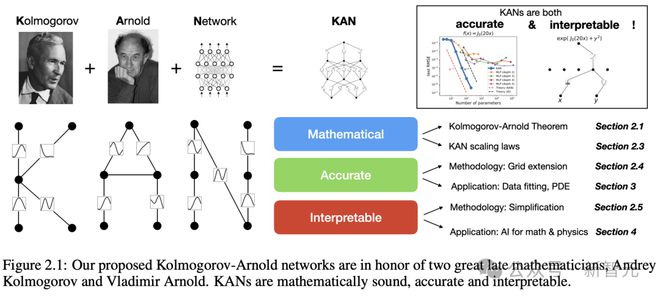
数学家 Andrey Kolmogorov 和 Vladimir Arnold
这个已经埋了 30 多年的数学原理,如今在 DL 时代被这位华人科学家和团队重新发现,再次发光发亮。

虽然,这项创新仅仅诞生了 5 个月的时间,但 KAN 已经在研究和编码社区,掀起了巨浪。
约翰霍普金斯大学计算机教授 Alan Yuille 赞扬道,KAN 更易于解释,可以从数据中提取科学规则,因此在科学领域中有着极大的应用」。
让不可能,成为可能
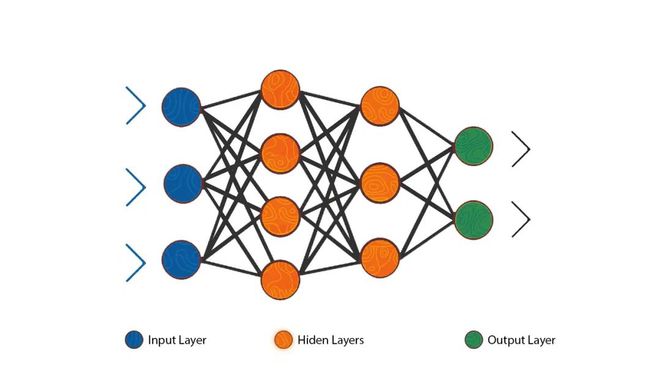
典型的神经网络工作原理是这样的:
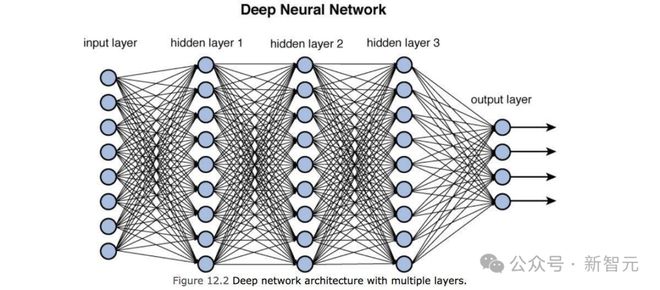
一层层人工神经元/节点,通过人工突触/边,进行连接。信息经过每一层,经过处理后再传输到下一层,直到最终将其输出。
对边进行加权,权重较大的边,比其他边有更大的影响。
在所谓的训练期间,这些权重会不断调整,最终使得神经网络输出越来越接近正确答案。
神经网络的一个常见的目标是,找到一种数学函数、曲线,以便最好地连接某些数据点。
它们越接近这个函数,预测的结果就越准确。
假设神经网络模拟了物理过程,理想情况下,输出函数将代表描述该物理过程的方程,相当于物理定律。
对于 MLP 来说,会有一个数学定理,告诉你神经网络能多接近最佳可能函数。
这个定理表明,MLP 无法完美地表示这个函数。
不过,在恰当的情况下,KAN 却可以做到。

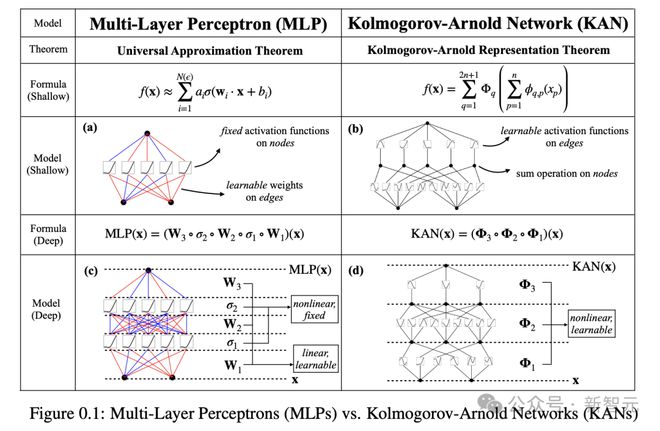
KAN 以一种不同于 MLP 的方式,进行函数拟合,将神经网络输出的点连接起来。
它不依赖于带有数值权重的边,而是使用函数。
同时,KAN 的边函数是非线性和可学习的,这使得它们比 MLP 更灵活、敏感。
然而,在过去的 35 年里,KAN 被认为在实际应用中,切不可行。
1989 年,由 MIT 物理学家转计算机神经科学家 Tomaso Poggio,共同撰写的一篇论文中明确指出:KAN 核心的数学思想,在学习神经网络的背景下是无关紧要的。
Poggio 的一个担忧,可以追溯到 KAN 核心的数学概念。

论文地址:http://cbcl.mit.edu/people/poggio/journals/girosi-poggio-NeuralComputation-1989.pdf
1957 年,数学家 Andrey Kolmogorov 和 Vladimir Arnold 在各自但相互补充的论文中证明——如果你有一个使用多个变量的单一数学函数,你可以把它转换成多个函数的组合,每个函数都有一个变量。

然而,这里有个一个重要的问题。
这个定理产生的单个变量函数,可能是「不平滑的」,意味着它们可能产生尖锐的边缘,就像V字的顶点。
这对于任何试图使用这个定理,重建多变量函数的神经网络来说,都是一个问题所在。
因为这些更简单的单变量部分,需要是平滑的,这样它们才能在训练过程中,学会正确地调增匹配目标值。
因此,KAN 的前景一直以来黯淡无光。
MIT 华人科学家,重新发现 KAN
直到去年 1 月,MIT 物理学研究生 Ziming Liu,决定重新探讨这个话题。
他和导师 Max Tegmark,一直致力于让神经网络在科学应用中,更加容易被人理解,能够让人们窥探到黑匣子的内部。
然而,这件事一直迟迟未取得进展。

可以说,在这种「走投无路」的情况下,Liu 决定在 KAN 上孤勇一试。
导师却在这时,泼了一盆冷水,因为他对 Poggio 论文观点太过熟悉,并坚持认为这一努力会是一个死胡同。
不过,Ziming Liu 却没有被吓到,他不想在没有先试一下的情况下,放弃这个想法。
随后,Tegmark 也慢慢改变了自己的想法。
他们突然认识到,即使由该定理产生的单值函数,是不平滑的,但神经网络仍可以用平滑的函数逼近数值。
Liu 似乎有一种直觉,认定了 KAN 便是那个拯救者。

因为自 Poggio 发表论文,已经过了 35 年,当下的软件和硬件取得了巨大的进步。
在 2024 年,就计算来讲,让许多事情成为可能。
大约肝了一周左右的时间,Liu 深入研究了这一想法。在此期间,他开发了一些原型 KAN 系统,所有系统都有两层。
因为 Kolmogorov-Arnold 定理本质上为这种结构提供了蓝图。这一定理,明确地将多变量函数分解为,不同的内部函数和外部函数集。
这样的排列,使其本身就具备内层和外层神经元的两层架构。
但令 Liu 沮丧的是,所设计的原型 KAN 并没有在科学相关任务上,表现地更好。
导师 Tegmark 随后提出了一个关键的建议:为什么不尝试两层以上的 KAN 架构,或许能够处理更加复杂的任务?
一语点醒梦中人。
这个开创性的想法,便成为他们突破的关键点。
这个羽翼未丰的原型架构,为他们带来了希望。很快,他们便联系了 MIT、加州理工、东北大学的同事,希望团队能有数学家,并计划让 KAN 分析的领域的专家。
实践证明,在 4 月份论文中,小组团证明了三层 KAN,确实是可行的。
他们给出了一个示例,三层 KAN 可以准确地表示一个函数,而两层 KAN 却不能。
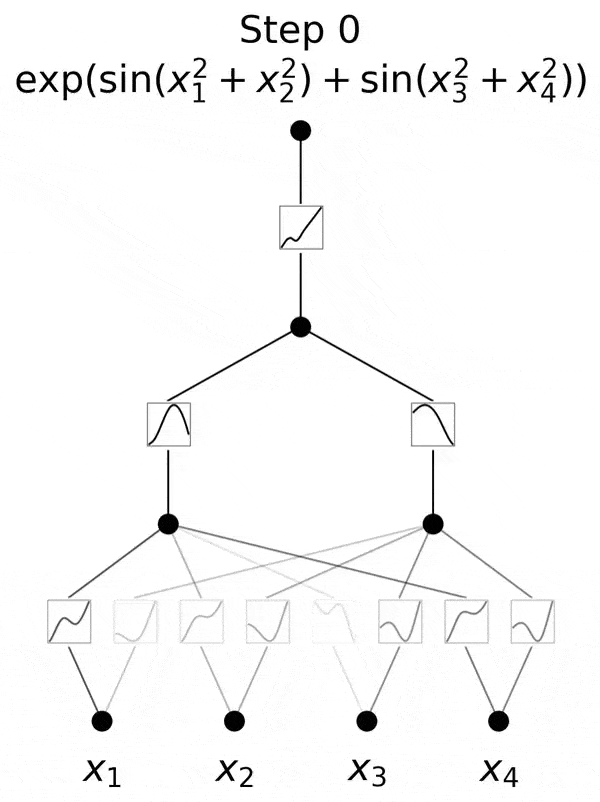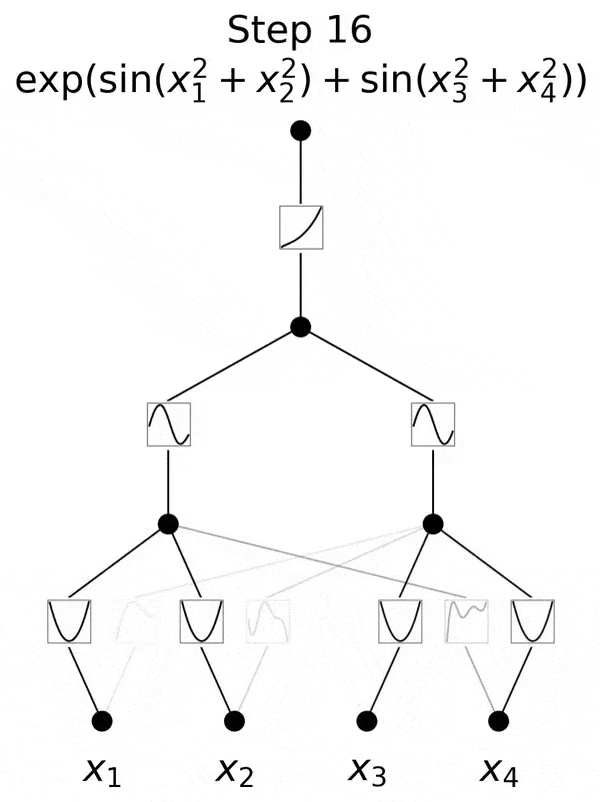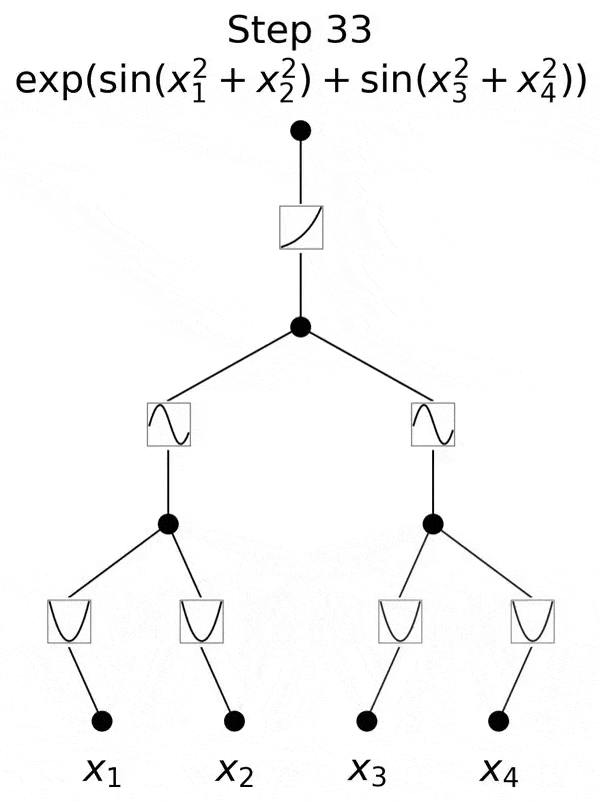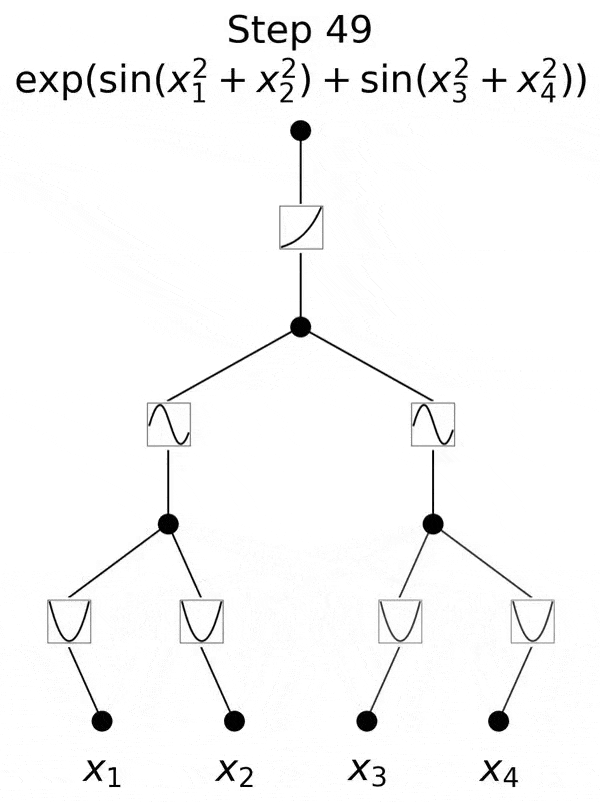
不过,研究团队并没有止步于此。自那以后,他们在多达六层的 KAN 上进行了实验,每一层,神经网络都能与更复杂的输出函数,实现对准。
论文合著作者之一 Yixuan Wang 表示,「我们发现,本质上,可以随心所欲堆叠任意多的层」。
发现数学定理碾压 DeepMind
更令人震惊的是,研究者在两个现实的世界问题中,对 KAN 完成了验证。
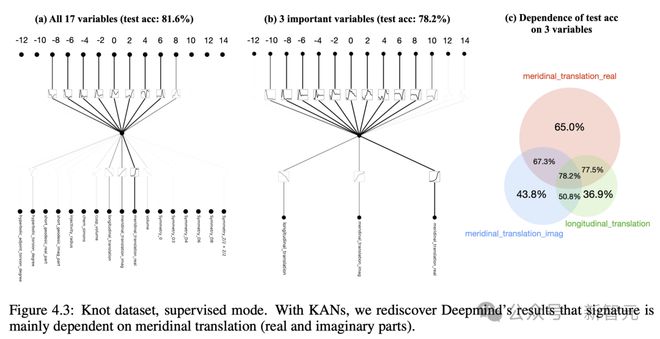
第一个,是数学一个分支中的「纽结理论」。
2021 年,DeepMind 团队曾宣布,他们已经搭建了一个 MLP,再获得足够纽结的其他属性后,可以预测出给定纽结的特定拓扑属性。
三年后,全新的 KAN 再次实现了这一壮举。

而且,它更进一步地呈现了,预测的属性如何与其他属性相关联。
论文一作 Liu 说,「这是 MLP 根本做不到的」。
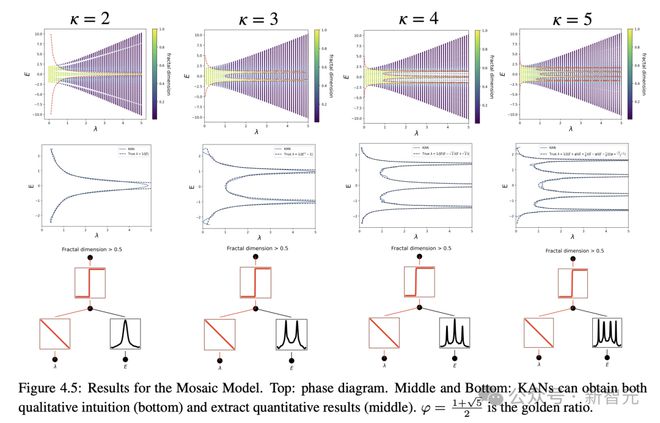
第二个问题是,设计凝聚态物理中的一种现象,称为 Anderson 局域化。
其目的是,预测特定相变将发生的边界,然后确定描述该过程的数学公式。同样,也只有 KAN 做到了在这一点。
Tegmark 表示,「但与其他形式的神经网络相比,KAN 的最大优势在于其可解释性,这也是 KAN 近期发展的主要动力」。
在以上的两个例子中,KAN 不仅给出了答案,还提供了解释。
他还问道,可解释性意味着什么?
「如果你给我一些数据,我会给你一个可以写在T恤上的公式」。
终极方程式?
KAN 这篇论文的出世,在整个 AI 圈引起了轰动。
AI 大佬们纷纷给予了高度的评价,有人甚至直呼,机器学习的新纪元开始了!

目前,这篇论文在短短三个月的时间里,被引次数近 100 次。
很快,其他研究人员亲自入局,开始研究自己的 KAN。
6 月,清华大学等团队的研究人员发表了一篇论文称,他们的 Kolmogorov-Arnold-informed neural network(KINN),在求解偏微方程(PDE)方面,明显优于 MLP。
对于研究人员来说,这可不是一件小事,因为 PED 在科学中的应用无处不在。
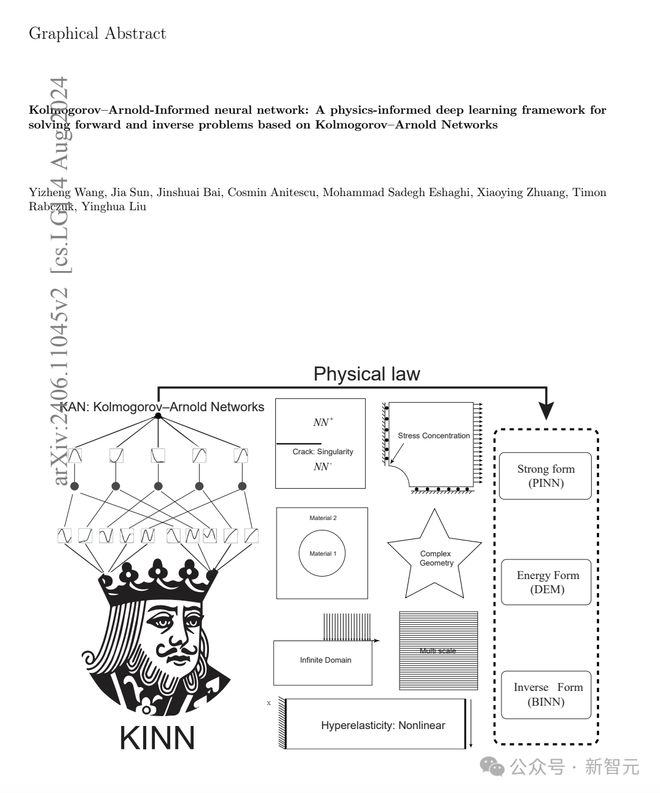
论文地址:https://arxiv.org/pdf/2406.11045
紧接着,7 月,来自新加坡国立大学的研究人员们,对 KAN 和 MLP 架构做了一个全面的分析。
他们得出结论,在可解释性的相关任务中,KAN 的表现优于 MLP,同时,他们还发现 MLP 在计算机视觉和音频处理方面做的更好。
而且,这两个网络架构在 NLP,以及其他 ML 任务上,性能大致相当。
这一结果在人意料之中,因为 KAN 团队的重点一直是——科学相关的任务,而且,在这些任务中,可解释性是首要的。

论文地址:https://arxiv.org/pdf/2407.16674
与此同时,为了让 KAN 更加实用、更容易使用。

8 月,KAN 原班人马团队再次迭代了架构,发表了一篇名为「KAN 2.0」新论文。

论文地址:https://arxiv.org/pdf/2408.10205
他们将其描述为,它更像是一本用户手册,而非一篇传统的论文。
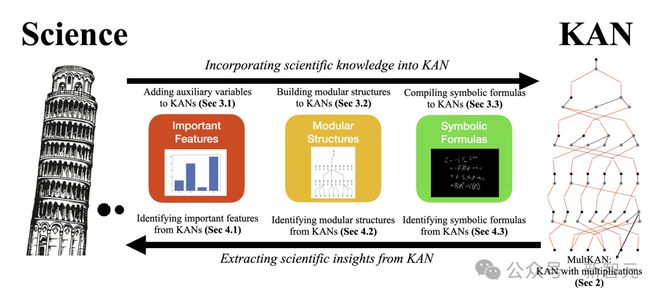
论文合著者认为,KAN 不仅仅是一种达到目的的手段,更是一种全新的科学研究方法。
长期以来,「应用驱动的科学」在机器学习领域占据主导地位,KAN 的诞生促进了所谓的「好奇心驱动的科学」的发展。
比如,在观察天体运动时,应用驱动型研究人员,专注于预测它们的未来状态,而好奇心驱动型研究人员,则希望揭示运行背后的物理原理。

Liu 希望,通过 KAN,研究人员可以从中获得更多,而不仅仅是在其他令人生畏的计算问题上寻求帮助。
相反,他们可能会把重点放在,仅仅是为了理解,而获得理解之上。
参考资料:






