
新智元报道
编辑:LRS
生成式模型原本被设计来模仿人类的各种复杂行为,但人们普遍认为它们最多只能达到与其训练数据中的专家相当的水平。不过,最新的研究突破了这一限制,表明在特定领域,如国际象棋,通过采用低温采样技术,这些模型能够超越它们所学习的那些专家,展现出更高的能力。
生成式模型(GMs)的设计宗旨是模仿人类的各种行为,例如回答问题、创作艺术、唱歌等,人类在这些领域都展现出高超的技能。
然而,模型在训练过程中实际上只专注于一个核心目标,即最小化模型输出的交叉熵损失,确保模型的输出分布尽可能地接近人类标注的分布。
换句话说,模型的能力上限可能已经被定死了,最多只能达到人类专家在其专业领域的表现水平。
但最近来自哈佛大学、加州大学圣巴巴拉分校(UCSB)、普林斯顿大学的研究结果表明,模型在某些特定的领域可以实现「超越(transcend)训练数据中的专家水平」的性能,青出于蓝而胜于蓝。

论文链接:https://arxiv.org/pdf/2406.11741
研究人员选择国际象棋作为研究目标展现模型的超越性(transcendence),因为其规则和玩法是清晰且有限的。
然后使用 Transformer 模型基于公开的人类国际象棋对局数据集进行训练,使其能够预测对局中的下一步走法。
为了探索模型是否能够超越人类专家,研究人员特意选择了一个没那么强的数据集,其中包含的人类玩家等级(使用 Glicko-2 对棋手等级进行评分)都不超过某个特定的分数。
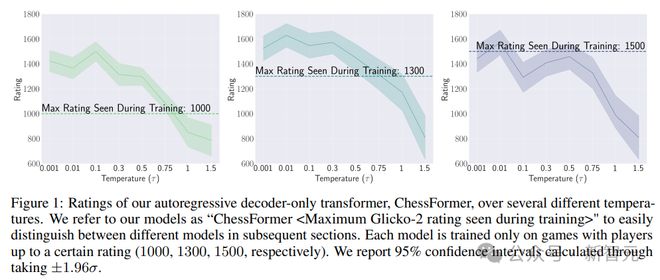
实验结果显示,模型不仅可以达到该分数,甚至部分模型还能实现性能超越,表明模型在某些情况下能够超越提供训练数据的人类专家。
该研究主要包括以下几个方面:
1. 在生成模型中形式化了超越(transcendence)的概念;
2. 通过将去噪专家的情况与模型集成联系起来,找到了解释超越的一个关键原因;
3. 在特定技能水平的玩家数据集上训练国际象棋 Transformer,并证实了模型在低温设置下能够超越其训练数据中专家的最高等级。
4. 通过降低采样温度,对奖励变化的分布进行可视化,并发现性能的提升主要归因于在相对较小的一部分状态下的大幅改进。
5. 探索了数据集多样性的必要性,以及在数据集不够多样化时模型无法实现超越的情况。
超越性的定义
研究人员首先描述了一个理论框架,用于构建和评估能够基于输入数据预测输出的机器学习模型:
1. 输入空间X和输出空间Y,其中X可以是任何长度,而Y是有限的。
2. 函数类F是所有将输入X映射到Y上概率分布的函数的集合,其中每个函数 f ∈ F 定义了给定输入x时输出y的条件概率。
3. 存在一个输入分布p,其对X中的所有输入都有非零概率。
4. 数据由k位专家进行标注,每位专家提供一个函数 fi,定义了给定输入x时输出y的概率分布。所有专家的分布被混合起来形成了一个混合分布。

5、由专家标注的过程生成的X和Y上的联合概率分布D。
6、奖励函数r,为每个输入-输出对分配一个奖励值
7、选择一个测试分布 ptest,并定义了在 ptest 上的平均奖励 Rptest (f),即对所有可能输出的奖励的期望值。
8、模型的目标是找到在联合分布D上的交叉熵损失最小的函数,其中交叉熵损失是衡量预测概率分布与真实概率分布差异的指标。
9、优化过程:学习者通过最小化交叉熵损失来选择最优的预测函数,包括对F中的所有可能函数进行评估和选择。
基于上述框架,超越性(transcendence)可以被定义为,在特定的函数设置和概率分布下,学习到的预测器在测试分布 ptest 上的平均奖励超过了所有专家(fi)中的最高奖励值。
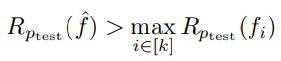
但这里讨论的是一个理想化的情况,学习器可以访问无限的数据,并且可以选择任何函数来拟合数据,不受架构或优化方法的限制。
不过,即使在这种理想化的条件下,如果没有对数据分布进行适当的修改,超越也可能是无法实现的。
在介绍这个理论框架时,研究人员做出了一些简化的假设,比如所有专家使用相同的输入分布,所有输入在训练分布下都有非零概率,专家是随机均匀选择的等等。
超越的条件
低温采样对于实现超越(transcendence)是必要的
在生成模型中,采样温度是一个控制生成过程随机性的参数。低温采样意味着模型在生成预测时更加确定,倾向于选择概率最高的输出,从而减少噪声和随机性,提高预测的准确性。
定理一:无论选择哪些专家函数和测试分布,总存在至少一个专家预测器,在测试分布上的奖励大于等于学习到的预测器。
当前的理论框架假设所有专家对于给定的输入x被均匀采样,即每个专家对输入x的预测被赋予相同的重要性。
未来也可以考虑使用贝叶斯加权,可以更有效地结合专家的意见,可能会提高预测器的性能。
使用低温度采样实现超越性
定理2:如果存在某个温度值在 0 到 1 之间,使得在这个温度值下或更低的温度下,通过温度采样得到的预测器的性能(即在测试分布上的奖励)高于所有专家,那么 argmax 预测器的性能也会高于所有专家。
低温采样可以被看作是在专家之间进行「多数投票」的过程,如果专家们对于最佳动作有显著的预测概率,那么通过多数投票得出的结果可能就会选择最佳动作。
当多个专家对最佳动作有共识时,这种共识可以通过多数投票被识别出来,从而提高整体的预测性能,体现了「群体的智慧」,即集体决策可能优于个体决策的现象。
通过这种方式,模型不仅复制了专家的知识,而且通过集体智慧提高了性能,实现了超越专家的预测。
对单个专家降噪
定理3:如果数据是由单个带噪声的专家生成的,那么存在某个温度在 (0, 1) 范围内,使得对于所有不超过的′,预测器能够实现超越。
在单一专家提供的数据中,即使存在噪声,通过低温采样也能够实现超越。
多专家超越
定理4:如果测试分布 test 不是集中在单一子集 Xi 上,即至少有两个不同的子集满足 test ()>0 和 test ()>0,那么在低温采样下,通过1,…,生成的数据可以实现超越。
只要测试分布不是只关注一个专家擅长的子集,而是涵盖了多个子集,那么通过低温采样,就可以实现超越。这是因为低温采样有助于集中概率质量在更可能的预测上,从而提高整体性能。
实验结果
研究的核心问题是探讨「低温采样是否能够在实践中真正引发超越现象」。
为了回答这个问题,研究人员测试了定理2,通过评估不同温度值下的多个 ChessFormer 模型,测试温度值的范围变化从 0.001(接近确定性)到 1.0(原始分布),再到 1.5(高熵)。
在图 1 中,作者明确证实了超越现象的存在。ChessFormer 1000 和 ChessFormer 1300 模型在温度τ等于 0.001 时能够实现大约 1500 的等级评分,展现出了超越现象。
通过调整采样温度,模型能够在某些情况下超越它们在训练期间所见过的最高等级。
研究人员还提出了两个问题来深入理解超越现象:奖励函数如何随低温采样而变化,以及超越是否依赖于数据集的多样性。
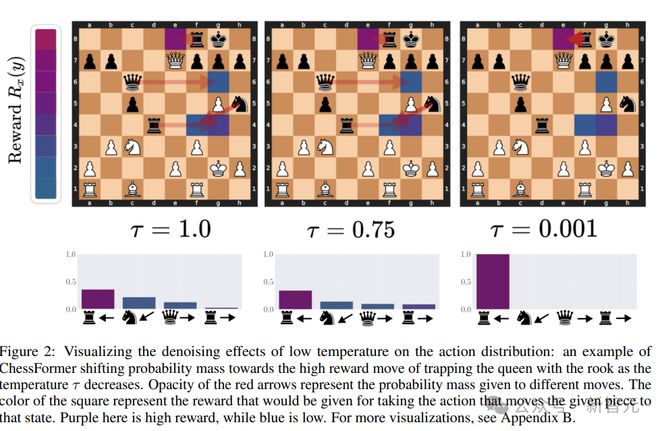
在棋类游戏中,技术水平较低的玩家可能在关键时刻犯下重大错误。如果这些错误具有个体差异,通过多个专家的预测平均化可以产生去噪效果,从而提高最佳走法的概率。
低温采样可以将概率质量转移到特定游戏情境中的更好走法上,从而提高预期奖励。
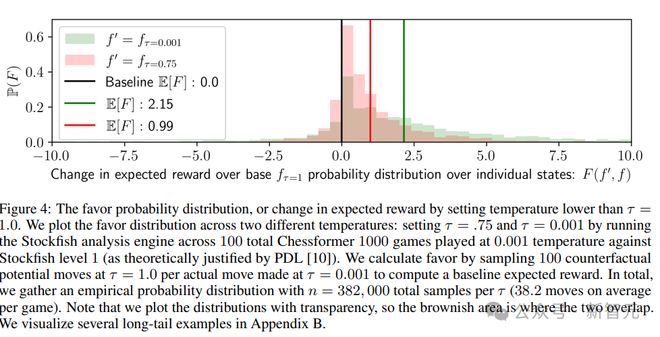
总之,实验和可视化结果强调了通过低温采样实现超越现象的潜力,并提出了研究问题来探索这一现象背后的机制。
参考资料:






