
新智元报道
编辑:LRS
白盒非监督学习模型性能再进一步!
最近马毅教授和图灵奖得主 Yann LeCun 联手在 ICLR 2023 上发表了一篇论文,描述了一种极简和可解释的非监督式学习方法,不需要求助于数据增强、超参数调整或其他工程设计,就可以实现接近 SOTA SSL 方法的性能。

论文链接: https://arxiv.org/abs/2209.15261
该方法利用了稀疏流形变换,将稀疏编码、流形学习和慢特征分析(slow feature analysis)相结合。
采用单层确定性稀疏流形变换,在 MNIST 上可以达到 99.3% 的 KNN top-1 精度,在 CIFAR-10 上可以达到 81.1% 的 KNN top-1 精度,在 CIFAR-100 上可以达到 53.2% 的 KNN top-1 精度。
通过简单的灰度增强,模型在 CIFAR-10 和 CIFAR-100 上的精度分别达到 83.2% 和 57% ,这些结果显著地缩小了简单的「白盒」方法和 SOTA 方法之间的差距。
此外,文中还提供了可视化解释如何形成一个无监督的表征变换。该方法与潜在嵌入自监督方法密切相关,可以看作是最简单的 VICReg 方法。

尽管在我们简单的建设性模型和 SOTA 方法之间仍然存在很小的性能差距,但有证据表明,这是一个有希望的方向,可以实现一个原则性的、白盒式的非监督式学习。
文章第一作者 Yubei Chen 是纽约大学数据科学中心(CDS)和 Meta 基础人工智能研究(FAIR)的博士后助理,导师为 Yann LeCun 教授,博士毕业于加州大学伯克利分校的 Redwood Center 理论神经科学和伯克利人工智能研究所(BAIR),本科毕业于清华大学。

主要研究方向研究为计算神经科学学习和深度无监督(自监督)学习的交叉,研究结果增强了对大脑和机器无监督表征学习的计算原理的理解,并重塑对自然信号统计的认识。
马毅教授于 1995 年获得清华大学自动化与应用数学双学士学位,并于 1997 年获加州大学伯克利分校 EECS 硕士学位,2000 年获数学硕士学位与 EECS 博士学位。目前是加州大学伯克利分校电子工程与计算机科学系教授,同时也是 IEEE Fellow,ACM Fellow,SIAM Fellow。

Yann LeCun 最著名的工作是在光学字符识别和计算机视觉上使用卷积神经网络(CNN),也被称为卷积网络之父;2019 年他同 Bengio 以及 Hinton 共同获得计算机学界最高奖项图灵奖。

从最简单的无监督学习开始
在过去的几年里,无监督表征学习取得了巨大的进展,并且有望在数据驱动的机器学习中提供强大的可扩展性。
不过什么是学习到的表征,以及它究竟是如何以无监督的方式形成的,这些问题仍然不清楚;此外,是否存在一套支撑所有这些无监督表征的共同原则仍不清楚。
许多研究者已经意识到提高模型理解力的重要性,并采取了一些开创性的措施,试图简化 SOTA 方法,建立与经典方法之间的联系,统一不同的方法,使表征可视化,并从理论角度分析这些方法,并希望能够开发出一种不同的计算理论:使我们能够基于第一原理从数据中建立简单的、完全可以解释的「白盒」模型,该理论也可以为理解人脑中无监督学习的原则提供指导。
在这项工作中,研究人员又朝着这个目标迈出了一小步,试图建立一个最简单的 「白盒」无监督学习模型,并且不需要深度网络、projection heads、数据增强或其他各种工程设计。
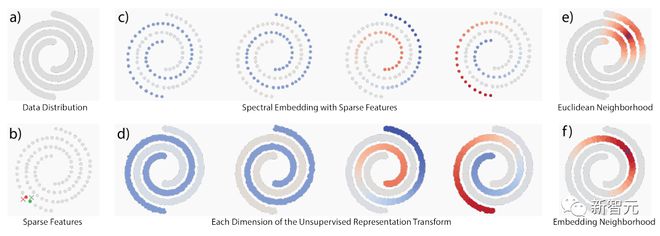
文中通过利用两个经典的无监督学习原则,即稀疏性(sparsity)和频谱嵌入(spectral embedding),建立了一个两层模型,在几个标准数据集上取得了非显著的基准结果。
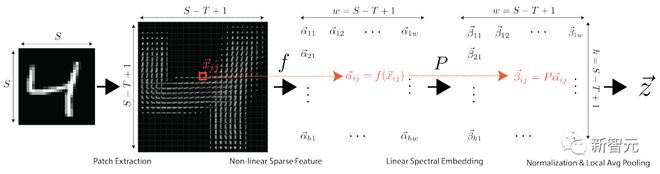
实验结果表明,基于稀疏流形变换(sparse manifold transform)的两层模型,与 latent-embedding 自监督方法具有相同的 objective,并且在没有任何数据增强的情况下,在 MNIST 上取得了 99.3% 的 KNN 最高 1 级准确率,在 CIFAR-10 上取得了 81.1% 的 KNN 最高 1 级准确率,在 CIFAR-100 上取得了 53.2% 的准确率。
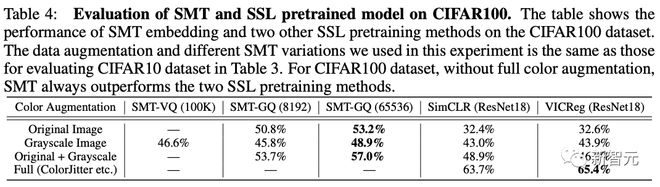
通过简单的灰度增强,进一步在 CIFAR-10 上实现了 83.2% 的 KNN top-1 精度,在 CIFAR-100 上实现了 57% 的 KNN top-1 精度。
这些结果为缩小「白盒」模型和 SOTA 自监督(SSL)模型之间的差距迈出了重要一步,虽然差距仍然很明显,但研究人员认为进一步缩小差距有可能对无监督表征的学习获得更深入的理解,这也是通往该理论实用化的一条有前景的研究路线。
三个基本问题
什么是无监督(自监督)的 re-presentation
从本质上讲,原始信号的任何非同一性转换(non-identity transformation)都可以被称为表征(re-presentation),不过学术界更感兴趣的是那些有用的转换。
无监督 re-presentation 学习的一个宏观目标是找到一个函数,将原始数据转换到一个新的空间,使「相似」的东西被放在更接近的地方;同时,新的空间不应该是一个 collapsed 且 trivial 的,也就是说,必须保留数据的几何或随机结构。
如果这一目标得以实现,那么「不相似」的内容自然会在表示空间中被放置得很远。
相似性(similarity)从何而来?
相似性主要来自三个经典的想法:1)时序共现,2)空间共现;和3)原始信号空间中的局部相邻(local neighborhoods)。
当基础结构为几何结构时,这些想法在相当程度上是重叠的;但当结构为随机结构时,它们在概念上也会有所不同,下图展现了流形结构(manifold structure)和随机共现结构(stochastic co-occurrence structure.)之间的区别。
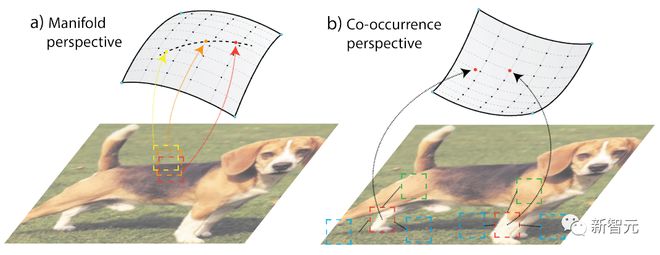
利用局部性,相关工作提出了两种无监督的学习方法:流形学习和共现统计建模,这些想法很多都达到了谱系分解的表述或密切相关的矩阵分解表述。
流形学习的理念是,只有原始信号空间中的局部邻域才是可信的,通过综合考虑所有的局部邻域,就会出现全局几何,即「全局思考,局部适配」(think globally, fit locally)。
相比之下,共现统计建模遵循一种概率理念,因为有些结构不能用连续流形来建模,所以它也是对流形理念的补充。
一个最明显的例子来自于自然语言,其中的原始数据基本不会来自于平滑的几何,比如在单词嵌入中,「西雅图」和「达拉斯」的嵌入可能很相似,尽管它们并没有频繁共现,其根本原因是它们有类似的上下文模式。
概率和流形的观点对于理解「相似性」是相互补充的 ,当有了相似性的定义后,就可以构造一个转换,使得相似的概念离得更近。
本文如何建立表征转换?基本原则:稀疏性和低秩(low rank)
大体上来说,可以用稀疏性来处理数据空间中的局部性和分解,以建立 support;然后用低频函数构建表征变换,将相似的值分配给 support 上的相似点。
整个过程也可以称为稀疏流形变换(sparse manifold transform)。
参考资料:






